Rates of change arise in many real-life situations, such as measuring how quickly water drains from a tub or how fast a car accelerates. Therefore, understanding the rate of change meaning is vital. It relates how one quantity varies in response to another. More specifically, AP® Calculus students encounter this concept everywhere, from growth and decay models to motion problems.

Moreover, the concept appears in “4.1 interpreting the derivative in context,” where the derivative becomes a powerful tool. A strong grasp of rates of change will help students make sense of graphical and numerical data. In addition, it forms the foundation upon which more advanced calculus ideas are built. Consequently, exploring the meaning of rate of change prepares students to interpret real-world phenomena using mathematical models.

Defining the Derivative as the Instantaneous Rate of Change

What Is an Instantaneous Rate of Change?

The derivative at a point is called the instantaneous rate of change. This formal idea provides the exact rate at which a function’s value changes with respect to its independent variable. Mathematically, for a function f(x), the derivative f'(x) is defined as:

f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}

This limit captures how fast f(x) changes at an exact point, rather than over a broad interval. Consequently, the derivative is linked to the tangent line’s slope at a particular value of x.

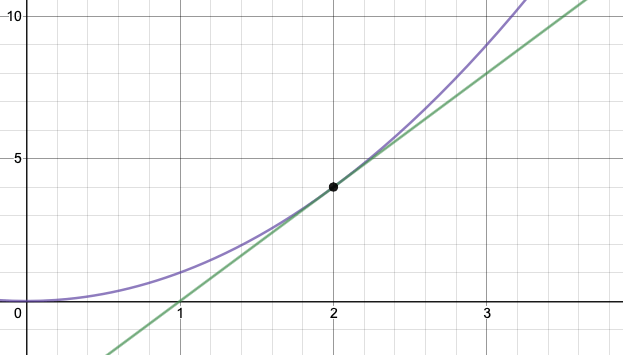
Simple Example (Step-by-Step)

Consider the function f(x) = x^2.

1. Write the function and identify the term to be differentiated: f(x) = x^2.
2. Use the power rule: If f(x) = x^n, then f'(x) = n \cdot x^{n-1}. Here, n=2.
3. Therefore, the derivative is: f'(x) = 2x.
4. Interpret the result: At any x, the instantaneous rate of change is 2x. For example, when x=3, the rate of change is 2 \cdot 3 = 6. This means the function’s value is increasing by 6 units per small step when x=3.

Practice Problem (Step-by-Step)

Find the derivative of g(x) = 3x^3 - 4x + 1.

1. Break down each term:
   • For 3x^3, apply the power rule to get 9x^2.
   • For -4x, the derivative is -4.
   • For 1, the derivative is 0.
2. Combine results: g'(x) = 9x^2 - 4.
3. Interpretation: At a point x=a, g'(a)= the instantaneous rate of change of g(x).

Using the Derivative to Express Information About Rates of Change

Applied Contexts and Real-World Interpretations

Many textbooks refer to velocity, where velocity is the rate of change of position. If position is described by a function s(t), then velocity equals s'(t). Likewise, if p(t) represents population at time t, then p'(t) tells how quickly the population grows or shrinks. Therefore, units become critical, since p'(t) might be in “people per year,” and s'(t) might be in “meters per second.”

Example in Context (Step-by-Step)

Suppose a population P(t) (in thousands) is given by P(t) = 200 \cdot e^{0.02t}, where t is time in years.

1. Compute the derivative: P'(t) = 200 \cdot 0.02 \cdot e^{0.02t} = 4 \cdot e^{0.02t}.
2. Interpret P'(t): It shows how rapidly the population (in thousands) changes each year.
3. For instance, at t=10 years, the rate of change is P'(10) = 4 \cdot e^{0.2}. Numerically, this is about 4 \times 1.2214 = 4.8856. Thus, the population is increasing by approximately 4.8856 thousand people per year at that instant.

Practice Problem (Step-by-Step)

A chemical reaction amount A(t) (in grams) is modeled by A(t) = 10 - 8e^{-0.5t}. Find the rate of change at t=5 minutes.

1. Differentiate:A'(t) = 0 - 8 \cdot (-0.5) \cdot e^{-0.5t} = 4e^{-0.5t}.
2. Evaluate at t=5:A'(5) = 4e^{-0.5 \cdot 5} = 4e^{-2.5}.
3. Approximate if desired: e^{-2.5} \approx 0.08208, so A'(5) \approx 4 \cdot 0.08208 \approx 0.32832 grams per minute.
4. Meaning: At minute 5, the chemical amount is increasing by about 0.32832 grams per minute.

Understanding Units: The Meaning of f'(x)

Relationship Between Units of f and x

In the expression f'(x), the units are crucial. The rate of change meaning includes a ratio of “units of f” over “units of x.” For example, if f(x) represents distance in meters and x represents time in seconds, then f'(x) is meters per second. Consequently, paying attention to units helps show whether the function is increasing or decreasing and how quickly that change happens.

Example Highlighting Units (Step-by-Step)

Imagine a function D(t), which gives the depth of water in a tank (in centimeters) after t hours. Let D(t) = 150 - 10t.

1. Differentiate: D'(t) = -10.
2. Specify units: D'(t) is -10 \frac{\text{cm}}{\text{hour}}.
3. Interpretation: The water level is dropping at a constant rate of 10 centimeters per hour. Therefore, after each hour, the depth decreases by 10 centimeters.

Practice Problem (Step-by-Step)

A temperature function T(x) is measured in degrees Celsius for an object moved between different rooms. Suppose

T(x) = 20 + 5x,

where x is time in minutes. Find the derivative and specify the units.

1. Differentiate: T'(x) = 5.
2. Identify unit meaning: T'(x) = 5 \frac{\text{°C}}{\text{minute}}.
3. Conclude: The object’s temperature rises at a constant rate of 5 degrees Celsius per minute.

Common Pitfalls and How to Avoid Them

Mixing Up Average vs. Instantaneous Rates of Change

It is easy to confuse average and instantaneous rates. The average rate of change of f(x) over [a,b] is:

\frac{f(b) - f(a)}{b - a}.

However, the instantaneous rate of change at x=a is given by f'(a). Therefore, be sure to identify whether a question asks for an average slope or the slope at a single point.

Neglecting Units in Applied Contexts

Many students forget to use units when reporting their answers. Unfortunately, this can lead to confusion in real-world scenarios. Always attach the correct units after each calculation, because the interpretation depends on understanding “what changes with respect to what.”

Quick Reference Chart: Key Terminology and Definitions

Term	Definition
Rate of Change	How one quantity changes in relation to another
Derivative f'(x)	The instantaneous rate of change of f(x) at a given x
Independent Variable	The variable upon which other quantities depend
Units of Derivative	Units of output (f) divided by units of input (x)
Average Rate of Change	Change in function value divided by the change in x over an interval

Conclusion

The rate of change meaning is a cornerstone of AP® Calculus because it provides deep insights into how functions change. Derivatives, in particular, reveal instantaneous rates of change, helping students interpret real-world processes. Therefore, close attention to “4.1 interpreting the derivative in context” strengthens problem-solving skills.

Meanwhile, consistent attention to units and context makes those insights even more powerful. This understanding guides success when tackling future calculus topics. Next steps might include examining higher-order derivatives or integrating the rate functions to find total changes over time. Mastery of these ideas builds a sturdy platform for advanced calculus studies.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.