Introduction

Many SAT® Math questions hide their solutions inside awkward radicals or bulky fractions. However, once an expression is rewritten into a friendlier form, the path to the answer often appears in seconds. Therefore, mastering the skill of rewriting rational and radical expressions helps students avoid algebra traps and earn quick points. This guide breaks the topic into bite-sized lessons, each supported by clear examples and SAT®-style practice.

Essential Building Blocks

A. Properties of Exponents

Remember these five rules:

• Product Rule: a^{m}\cdot a^{n}=a^{m+n}
• Quotient Rule: \dfrac{a^{m}}{a^{n}}=a^{m-n}
• Power Rule: \left(a^{m}\right)^{n}=a^{mn}
• Zero Exponent Rule: a^{0}=1 (if a\neq 0)
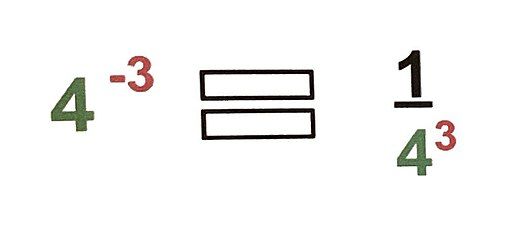
• Negative Exponent Rule: a^{-n}=\dfrac{1}{a^{n}}

B. Radical–Exponent Connection

Every radical can be rewritten with a rational exponent.

• Square root: \sqrt{a}=a^{1/2}
• General form: \sqrt[n]{a^{m}}=a^{m/n}

Example

Rewrite \sqrt[5]{x^{3}} as a rational exponent.

Solution: \sqrt[5]{x^{3}} = x^{3/5}

Converting Between Radical & Rational Exponent Form

Switching forms often shortens calculations, especially on the SAT® calculator section.

1. Identify the index (root) n and the power m.
2. Write the base with exponent \frac{m}{n}.
3. If needed, evaluate using exponent rules or your calculator.

Example

Rewrite and evaluate 32^{3/5}.

1. Note that 32 = 2^{5}.
2. Therefore, 32^{3/5} = \left(2^{5}\right)^{3/5}=2^{(5)(3/5)}=2^{3}.
3. Final value: 2^{3}=8

Simplifying Radical Expressions

A. Product & Quotient Properties of Radicals

• Product: \sqrt{ab}=\sqrt{a}\cdot\sqrt{b} if a,b\ge 0.
• Quotient: \sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}} if b>0.

B. Rationalizing Denominators

1. Is there a single-term root in the denominator? Multiply the numerator and denominator by that root.
2. Is there a binomial with a root? Multiply the numerator and denominator by the conjugate.

Example

Simplify \dfrac{\sqrt{50}}{\sqrt{2}}.

Step 1: Combine under one radical by the quotient property.

\dfrac{\sqrt{50}}{\sqrt{2}}=\sqrt{\dfrac{50}{2}}

Step 2: Divide inside.

\sqrt{25}=5

Answer: 5

Example

Rationalize \dfrac{3}{2+\sqrt{5}}.

Step	Reason
\dfrac{3}{2 + \sqrt{5}}	Original expression
\dfrac{3(2 - \sqrt{5})}{(2 + \sqrt{5})(2 - \sqrt{5})}	Multiply by the conjugate of the denominator
\dfrac{6 - 3\sqrt{5}}{4 - 5}	Expand the numerator and use the difference of squares in denominator
\dfrac{6 - 3\sqrt{5}}{-1}	Simplify the denominator
-6 + 3\sqrt{5}	Final simplified expression ✅

Simplifying Rational Expressions

A. Factoring Toolbox

• Greatest Common Factor (GCF)
• Difference of Squares: a^{2}-b^{2}=(a+b)(a-b)
• Trinomials: Factor into two binomials when possible.

B. Canceling Common Factors & Domain Restrictions

After factoring, cancel only factors, never terms. However, every canceled factor still creates a restriction (value that makes a denominator zero).

Example

Simplify \dfrac{x^{2}-9}{x^{2}-x-6} and state restrictions.

Step	Reason
\dfrac{x^{2} - 9}{x^{2} - x - 6}	Original expression
\dfrac{(x - 3)(x + 3)}{(x - 3)(x + 2)}	Factor the numerator and denominator
\dfrac{\cancel{(x - 3)}(x + 3)}{\cancel{(x - 3)}(x + 2)}	Cancel common factor (x−3)
\dfrac{x + 3}{x + 2}	Final simplified expression ✅

Restrictions: The factors of the denominator give x\neq 3 and x\neq -2.

Combining Radical & Rational Techniques

Mixed expressions may need both exponent conversion and factoring.

Strategy Checklist

1. Convert radicals to rational exponents.
2. Factor any polynomials.
3. Cancel common factors.
4. Rationalize denominators if radicals stay below.

Example

Simplify \dfrac{\sqrt{x^{4}y}}{\sqrt{xy^{3}}}.

Step	Reason
\dfrac{\sqrt{x^{4}y}}{\sqrt{xy^{3}}}	Original expression
\sqrt{\dfrac{x^{4}y}{xy^{3}}}	Use property: \dfrac{\sqrt{a}}{\sqrt{b}} = \sqrt{\dfrac{a}{b}}
\sqrt{\dfrac{x^{4}}{x} \cdot \dfrac{y}{y^{3}}} = \sqrt{x^{3} \cdot y^{-2}}	Simplify inside the radical
x^{3/2} \cdot y^{-1}	Convert to exponent form
\dfrac{x^{3/2}}{y}	Final expression in exponent form
\dfrac{x\sqrt{x}}{y}	Final expression in radical form ✅

Common SAT® Traps & Time-Saving Tips

• Extraneous Solutions: Squaring both sides can introduce answers that do not fit the original equation. Always check.
• Hidden Factors: Substitution, such as letting u=\sqrt{x}, can reveal a quadratic waiting to be factored.
• Estimation: If answer choices are numerical, compare rough radical values (e.g., \sqrt{5}\approx2.2) to eliminate options quickly.

Example

Solve \sqrt{x+3}=x+1.

Step	Reason
\sqrt{x + 3} = x + 1	Original equation
(\sqrt{x + 3})^2 = (x + 1)^2	Square both sides
x + 3 = x^2 + 2x + 1	Simplify both sides
0 = x^2 + x - 2	Rearrange into standard form
0 = (x + 2)(x - 1)	Factor the quadratic
x = -2\quad\text{or}\quad x = 1	Solve for x
\text{Check } x = -2: \\ \sqrt{-2 + 3} = 1 \Rightarrow -2 + 1 = -1	❌ Reject extraneous solution
\text{Check } x = 1: \\ \sqrt{1 + 3} = 2 \Rightarrow 1 + 1 = 2	✅ Valid solution

Quick Reference Chart

Term	Definition	Helpful Hint
Rational Exponent	An exponent expressed as a fraction, such as 2^{3/4}.	Denominator = root, numerator = power.
Radical	Expression containing a root symbol, e.g., \sqrt{7}.	Rewrite as exponent \frac{1}{2} to use exponent rules.
Conjugate	For a+b\sqrt{c}, the conjugate is a-b\sqrt{c}.	Product removes the radical.
Domain Restriction	Values that make a denominator zero or a negative inside even roots.	State after simplifying rational expressions.
Factor	A quantity multiplied to form a product.	Only factors (not terms) cancel in fractions.

Short Practice Set with Answers

1. Rewrite \sqrt[3]{16} using a rational exponent and evaluate.
   
2. Simplify \dfrac{\sqrt{27}}{3}.
   
3. Rationalize and simplify \dfrac{5}{\sqrt{3}}.
   
4. Simplify \dfrac{2x^{2}+6x}{4x} and state restrictions.

Answers

1. 2\sqrt[3]{2}
2. \sqrt{27}=3\sqrt{3}\Rightarrow \dfrac{3\sqrt{3}}{3}=\sqrt{3}.
3. \dfrac{5\sqrt{3}}{3}.
4. \frac{x+3}{2}. Restriction: x\neq 0.

Final Takeaways & Next Steps

Rewriting rational and radical expressions turns intimidating problems into routine exercises, which leads to faster and more accurate SAT® Math answers. Therefore, keep practicing the conversion, factoring, and rationalizing skills highlighted above. Next, try a full set of mixed problems from reliable SAT® prep resources to cement these strategies.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.