Introduction

Right triangles show up on nearly every SAT® Math exam. When a problem involves ladders, ramps, or slanted roofs, right triangle trigonometry​ is usually the hidden tool. By the end of this guide, students will be able to:

• Apply the Pythagorean Theorem with confidence
• Use SOH-CAH-TOA in both calculator and non-calculator sections
• Recognize and exploit 30-60-90 and 45-45-90 special right triangles

Therefore, score-boosting shortcuts will feel natural.

Pythagorean Theorem Refresher

A. Formula and Quick Facts

For any right triangle, the squares of the legs add to the square of the hypotenuse:

a^{2}+b^{2}=c^{2}

Key points:

• The hypotenuse is always opposite the 90^\circ angle.
• If two sides are known, the third follows quickly.
• Common SAT® leg lengths include 3-4-5, 5-12-13, and their multiples.

B. Common SAT® Twists

1. Legs with radicals: 5\sqrt{2} often pairs with 5\sqrt{2} in isosceles right triangles.
2. Missing hypotenuse in coordinate plane distance questions.
3. Hidden right angles are created by altitude lines or slopes.

C. Example

Points A (–2, 3) and B (4, –1) form two vertices of a right triangle with the right angle at A. Find the length of the hypotenuse \overline{AB}.

Solution

1. Identify the legs using the distance in x and y directions.

• Change in x = |4 – (–2)| = 6
• Change in y = |–1 – 3| = 4

2. Because the right angle is at A, those lengths are legs. Therefore:

a=6,b=4

3. Apply the theorem:

6^{2}+4^{2}=c^{2}

36+16=c^{2}

52=c^{2}

c=\sqrt{52}=2\sqrt{13}

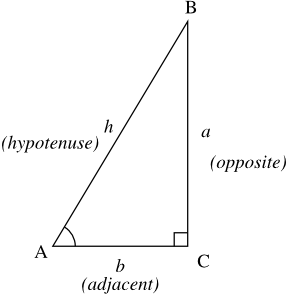
Meet SOH-CAH-TOA: The Core of Right Triangle Trigonometry

A. Defining Sine, Cosine, and Tangent

For an acute angle θ in a right triangle:

• Sine: \sin\theta=\dfrac{\text{opposite}}{\text{hypotenuse}}
• Cosine: \cos\theta=\dfrac{\text{adjacent}}{\text{hypotenuse}}
• Tangent: \tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}

The mnemonic “SOH-CAH-TOA” summarizes these ratios.

B. Setting Up Ratios

First, label the triangle relative to angle θ. Next, assign each given length to the opposite, adjacent, or hypotenuse. Finally, substitute into the correct ratio.

C. Calculator vs. Non-Calculator Sections

• Non-calculator: angles of 30^\circ, 45^\circ, 60^\circ dominate. Memorize their exact values.
• Calculator: Any angle may appear, yet set the device to degree mode.

D. Example

Problem

In right triangle RST, m\angle T = 90^\circ and leg RS = 8 cm. If m\angle R = 37^\circ, find RT to the nearest tenth.

Solution

Use the cosine function:

\cos(\angle R) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{RT}{RS}

Substitute the known values:

\cos(37^\circ) = \dfrac{RT}{8}

Now solve for RT:

RT = 8 \times \cos(37^\circ) RT \approx 8 \times 0.7986 = 6.4 \text{ cm}

Complementary Angles: The Sine-Cosine Link

Because the acute angles in a right triangle are complementary, \theta + (90^{\circ}-\theta)=90^{\circ}. Consequently,

\sin\theta=\cos(90^{\circ}-\theta)\cos\theta=\sin(90^{\circ}-\theta)

Quick Example

If \cos25^{\circ}=0.9063, then \sin65^{\circ} must also equal 0.9063. No calculator required!

Special Right Triangles Cheat Sheet

A. 45-45-90 Triangles

1. Pattern: sides are x,,x,,x\sqrt{2} (legs, leg, hypotenuse).
2. Derivation: An isosceles right triangle splits a square diagonally.
3. Example
   • Problem
     • The legs of an isosceles right triangle measure 7 cm. Find the hypotenuse.
   • Solution
     • c=7\sqrt{2}\text{ cm}.

B. 30-60-90 Triangles

1. Pattern: x,;x\sqrt{3},;2x (short leg, long leg, hypotenuse).
2. Derivation: drop an altitude in an equilateral triangle of side 2x.
3. Example
   • Problem
     • The long leg of a 30-60-90 triangle is 9\sqrt{3}. Determine the other two sides.
   • Solution
     • Long leg = x\sqrt{3} → x=9.
     • Short leg = x=9; hypotenuse = 2x=18.

Using Similarity to Build Exact Trig Values

By placing special right triangles on the unit circle, exact ratios follow.

Angles	Sine	Cosine	Tangent
30^\circ	\dfrac{1}{2}	\dfrac{\sqrt{3}}{2}	\dfrac{\sqrt{3}}{3}
45^\circ	\dfrac{\sqrt{2}}{2}	\dfrac{\sqrt{2}}{2}	1
60^\circ	\dfrac{\sqrt{3}}{2}	\dfrac{1}{2}	\sqrt{3}

Example

Find \sin45^{\circ}.

Solution: In a 45-45-90 triangle with legs 1, hypotenuse \sqrt{2},

\sin45^{\circ}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}

Strategy Section: Which Tool When?

Decision bullets guide quick choices:

• Need a missing side and have the other two? → Use Pythagorean Theorem.
• Know one side and one non-right angle? → Apply SOH-CAH-TOA.
• Angle equal to 30^\circ, 45^\circ, 60^\circ? → Special triangle shortcuts save time.
• Asked for exact value, not decimal? → Prefer special triangles or similarity.

Timed-test tips: Write the SOH-CAH-TOA letters on scrap paper immediately; it prevents mix-ups under pressure.

Real-World & SAT®-Style Applications

1. Angle of Elevation

Problem

A surveyor stands 40 m from a tower. The line of sight to the top forms a 33^\circ angle of elevation. Estimate the tower’s height to the nearest meter.

Solution

Opposite = height, adjacent = 40 m.

\tan33^{\circ}=\dfrac{h}{40} → h=40\tan33^{\circ}\approx40(0.649)=26\text{ m}

2. Coordinate Plane Tie-In

Problem

Triangle PQR has right angle at Q with Q(3, –2) and R(7, 5). If PQ = 5, find PR.

Solution

1. Find QR using distance formula:
   • Δx = 7 – 3 = 4, Δy = 5 – (–2) = 7 → QR=\sqrt{4^{2}+7^{2}}=\sqrt{65}.
2. Apply the Pythagorean Theorem to the triangle:
   • pq^{2}+(QR)^{2}=(PR)^{2}
   • 5^{2}+65=(PR)^{2}
   • 25+65=90 → PR=\sqrt{90}=3\sqrt{10}.

Quick Reference Vocabulary Chart

Term	Definition
Hypotenuse	The side opposite the right angle; longest side.
Opposite Side	The side across from a given acute angle.
Adjacent Side	The side next to a given acute angle (not the hypotenuse).
Altitude	A perpendicular segment from a vertex to the opposite side.
Angle of Elevation	The angle formed by a horizontal line and a line of sight upward.
Angle of Depression	The angle formed by a horizontal line and a line of sight downward.
Complementary Angles	Two angles whose measures add to 90^\circ.
Similar Triangles	Triangles with equal corresponding angles and proportional sides.

Practice Questions

1. A right triangle has legs 9 cm and 12 cm. Find the hypotenuse.
2. In △XYZ, m\angle Y = 90^\circ, XY = 10 m, m\angle X = 28^\circ. Find YZ to the nearest tenth.
3. Find \cos60^{\circ} using a special triangle.
4. The hypotenuse of a 30-60-90 triangle is 14. What is the shorter leg?
5. \angle A and \angle B are complementary. If \sin A=0.8, what is \cos B?

Answer Key with Brief Explanations

1. 15
2. 10\sin28^{\circ}\approx4.7\text{ m}
3. \cos60^{\circ}=\dfrac{1}{2}.
4. 7.
5. 0.8.

Key Takeaways & Next Steps

• Memorize the Pythagorean triple patterns (3-4-5, 5-12-13).
• Keep SOH-CAH-TOA written out until it sticks.
• Special right triangles convert angles 30^\circ, 45^\circ, 60^\circ into speedy exact values.
• The sine of an angle equals the cosine of its complement.
• Practice daily; short bursts of study reinforce retention more than cramming.

Next, tackle official SAT® practice sets and time every attempt. With the strategies above, right triangle trigonometry will become a reliable strength. Good luck!

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.