Derivatives are a core concept in calculus and describe how a function changes. They form the foundation for many topics in advanced mathematics. However, the exploration does not stop at the first derivative. Instead, it extends to the second derivative and beyond, offering deeper insights into a function’s behavior. Therefore, seeing why the second derivative notation is important can help in understanding concavity, acceleration, and other real-world applications.
Furthermore, higher-order derivatives bring clarity to even more complex changes in dynamic systems. This discussion will introduce the first derivative, explain the second derivative in detail using standard second derivative notation, and then highlight the usefulness of taking derivatives to even higher orders.
What We Review
Recap of First Derivatives
The first derivative describes the rate of change of a function. For a function f(x), the first derivative is often written in a few common ways:
- f'(x)
- \frac{dy}{dx} (if y = f(x))
- \frac{d}{dx}\bigl(f(x)\bigr)
The first derivative measures how fast a quantity changes at any given point. Therefore, it shows the slope of the function or the speed of an object in motion, depending on the context.
For example, if f(x) describes the distance of a car over time, then f'(x) describes its instantaneous velocity at any moment.
Exploring the Second Derivative
Definition and Second Derivative Notation
The second derivative is the derivative of the first derivative. In other words, it investigates how the rate of change itself changes. This quantity is denoted with:
- f''(x)
- \frac{d^2y}{dx^2}
- y''
Because it considers the curvature (or concavity) of a function, the second derivative often appears in real-life scenarios involving acceleration. When f(x) represents position, its first derivative f'(x) represents velocity, and its second derivative f''(x) represents acceleration.
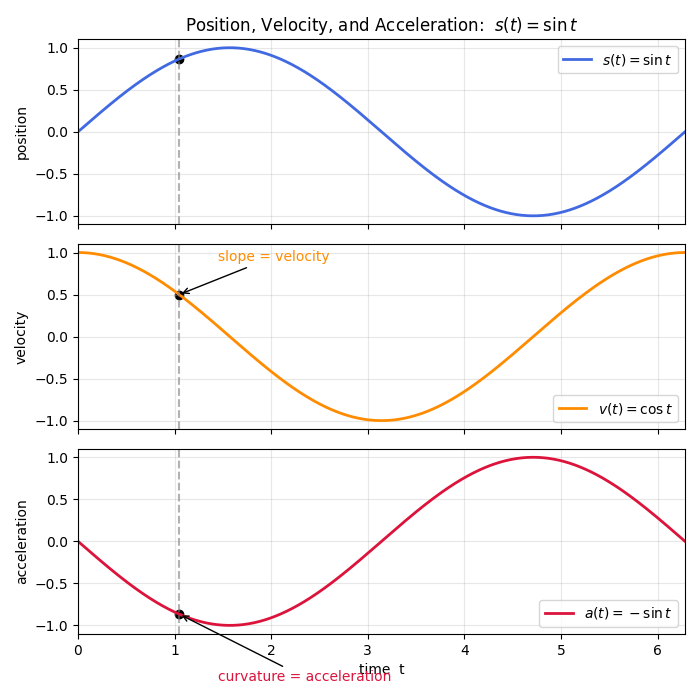
Step-by-Step Example: Finding the Second Derivative
Consider the function f(x) = 3x^3 - 2x^2 + 5x - 4. The goal is to find f''(x).
- First, find the first derivative f'(x).
- Differentiate 3x^3 to get 9x^2.
- Differentiate -2x^2 to get -4x.
- Differentiate 5x to get 5.
- Differentiate -4 to get 0.
- Therefore, f'(x) = 9x^2 - 4x + 5.
- Next, find the second derivative f''(x).
- Differentiate 9x^2 to get 18x.
- Differentiate -4x to get -4.
- Differentiate 5 to get 0.
- Therefore, f''(x) = 18x - 4.
Hence, f''(x) is the measure of how the slope, f'(x), is changing.
Delving into Higher-Order Derivatives
Definition of Higher-Order Derivatives
Higher-order derivatives go beyond the second derivative. The third derivative, for instance, is f^{(3)}(x), and so on. More generally, the n-th derivative is denoted by:
- f^{(n)}(x)
- \frac{d^n y}{dx^n}
These higher-order derivatives become important for analyzing complex motion, rates of change in dynamic systems, and even approximations in Taylor series.
When and Why Higher-Order Derivatives Are Useful
- Physics: The third derivative often helps study the rate of change of acceleration, known as “jerk.”
- Engineering: Higher-order derivatives can improve accuracy in predicting how mechanical systems respond to forces.
- Economics: Rate changes in supply and demand can be analyzed with second or third derivatives to see trends more clearly.
Step-by-Step Example: Finding a Third Derivative
Consider the function g(x) = 5x^4 - x^3 + 4x^2 - 7. The task is to find the third derivative, g^{(3)}(x).
- First, find the first derivative g'(x).
- Differentiate 5x^4 to get 20x^3.
- Differentiate -x^3 to get -3x^2.
- Differentiate 4x^2 to get 8x.
- Differentiate -7 to get 0.
- Thus, g'(x) = 20x^3 - 3x^2 + 8x.
- Next, find the second derivative g''(x).
- Differentiate 20x^3 to get 60x^2.
- Differentiate -3x^2 to get -6x.
- Differentiate 8x to get 8.
- Thus, g''(x) = 60x^2 - 6x + 8.
- Finally, find the third derivative g^{(3)}(x).
- Differentiate 60x^2 to get 120x.
- Differentiate -6x to get -6.
- Differentiate 8 to get 0.
- Thus, g^{(3)}(x) = 120x - 6.
This process can continue for fourth or higher orders as needed, especially in advanced studies of motion or change.
Quick Reference Chart (Vocabulary and Definitions)
| Term | Definition |
| Derivative | The rate of change of a function with respect to its variable, such as f'(x). |
| Second Derivative | The derivative of the first derivative, such as f''(x), measuring how f'(x) changes. |
| Higher-Order Derivatives | Derivatives beyond the second, like f^{(3)}(x) or f^{(4)}(x). |
Conclusion
Second derivative notation is a key foundation that extends the idea of change to how the rate of change itself evolves. By revealing a function’s concavity or the acceleration of an object, the second derivative is useful in both abstract math problems and tangible real-world scenarios.
In summary, higher-order derivatives expand on this idea further and enable deeper exploration of dynamic systems. This process underpins more advanced calculus topics in physics, engineering, and other fields. It is helpful to keep practicing derivative rules and techniques in order to see how each higher order comes into play.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.
