The Fundamental Theorem of Calculus is central to understanding how differentiation and integration are connected. It has two main parts: Part 1 links the derivative of an integral to the original function, and Part 2—often called the second fundamental theorem of calculus—explains how to quickly find definite integrals once an antiderivative is known. This second part is especially useful for avoiding long calculations using sums.
Next, it is important to notice how the second fundamental theorem of calculus shows up in the AP® Calculus AB-BC curriculum. Students encounter it when learning about continuity and antiderivatives under FUN-6.B.1, FUN-6.B.2, and FUN-6.B.3. Therefore, having a clear understanding of all these components will help build a strong foundation for more advanced topics.
What We Review
Key Concepts Review
Definition of an Antiderivative
An antiderivative of a function f(x) is a new function g(x) whose derivative is the original function. In other words, if f(x) is given, then g(x) is an antiderivative if g'(x) = f(x). Therefore, knowing how to find antiderivatives is essential before using the fundamental theorem of calculus part 2.
Continuous Functions on an Interval
In order for the theorem to work, f(x) must be continuous on the interval of integration. If the function has any breaks or jumps, the result could fail. Consequently, we often define a function F(x) as:\displaystyle F(x) = \int_{a}^{x} f(t)dtwhere f is continuous on [a,x]. This setup paves the way for applying the second fundamental theorem of calculus.
The Fundamental Theorem of Calculus, Part 2 (Second Fundamental Theorem of Calculus)
Part 2 states that if f(x) is continuous on [a, b] and F(x) is any antiderivative of f(x), then:\displaystyle \int_{a}^{b} f(x)dx = F(b) - F(a)
This formula offers a simpler route to compute definite integrals without dealing directly with sums and limits. Remember that a definite integral refers to the signed area under a curve. This is reinforced in the image below, where the area above the x-axis is positive, and the area below the x-axis is negative.
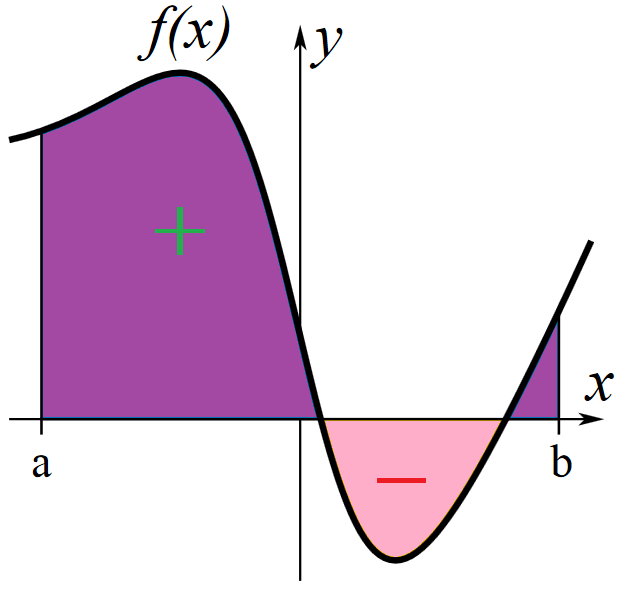
Understanding the Second Fundamental Theorem of Calculus
Intuitive Explanation
The second fundamental theorem of calculus is powerful because it places the integral and the derivative under one umbrella. Instead of struggling with infinite Riemann sums, students can find a function F(x) whose derivative is f(x). Then, to evaluate the definite integral, only the values F(b) and F(a) are needed. This shortcut means a lot of time saved on problems that could otherwise become very complicated.
Relation to Real-World Problems
In many real-world situations, f(x) might represent a rate of change. Therefore, the definite integral \int_{a}^{b} f(x)dx can represent the total change in some quantity from x = a to x = b. Accumulation problems in physics, biology, and economics often depend on this principle. Hence, applying the fundamental theorem of calculus part 2 is crucial for finding exact values with relative ease.
Step-by-Step Examples
Example 1: Basic Polynomial Function
1. Problem Statement
Evaluate \displaystyle \int_{2}^{5} x^2dx using the second fundamental theorem of calculus.
2. Steps to Solve
- Find an antiderivative of x^2. One antiderivative is \displaystyle \frac{x^3}{3}.
- Evaluate \displaystyle \frac{x^3}{3} at the upper limit x=5 and at the lower limit x=2.
- Subtract the value at 2 from the value at 5. So, first calculate: \displaystyle \frac{5^3}{3} = \frac{125}{3} Next, calculate: \displaystyle \frac{2^3}{3} = \frac{8}{3} Then, subtract: \displaystyle \frac{125}{3} - \frac{8}{3} = \frac{117}{3} = 39
3. Final Answer \displaystyle 39
Example 2: Simple Exponential Function
1. Problem Statement
Evaluate \displaystyle \int_{0}^{1} e^xdx using the second fundamental theorem of calculus.
2. Steps to Solve
- Recognize that an antiderivative of e^x is e^x.
- Compute e^1 and e^0.
- Subtract the value at 0 from the value at 1. First, evaluate at x=1: \displaystyle e^1 = e Then, at x=0: \displaystyle e^0 = 1 Finally, subtract: \displaystyle e - 1
3. Final Answer \displaystyle e - 1
Example 3: Trigonometric Function
1. Problem Statement
Evaluate \displaystyle \int_{0}^{\frac{\pi}{2}} \sin xdx using the second fundamental theorem of calculus.
2. Steps to Solve
- Recall that an antiderivative of \sin x is -\cos x.
- Evaluate -\cos x at x = \frac{\pi}{2} and x = 0.
- Subtract the smaller x-value result from the larger x-value result. First, evaluate at x = \frac{\pi}{2}: \displaystyle -\cos\left(\frac{\pi}{2}\right) = -0 = 0 Then, at x = 0: \displaystyle -\cos(0) = -1 Therefore, subtract:\displaystyle 0 - (-1) = 1
3. Final Answer \displaystyle 1
Common Pitfalls and How to Avoid Them
- Forgetting the “Plus C.” Because definite integrals subtract the antiderivative values at the boundaries, any constant cancels out. Thus, it does not affect the final result.
- Handling Negative Boundaries or Reverse Limits. Remember that \displaystyle \int_{b}^{a} f(x)dx = -\int_{a}^{b} f(x)dx. Therefore, pay close attention to the order of limits.
- Checking Continuity. Always confirm that the function f(x) is continuous on the interval [a, b]. If there is a discontinuity, additional techniques or breaks in the integral may be required.
Quick Reference Chart
| Term | Definition/Explanation |
| Antiderivative | A function G(x) such that G'(x) = f(x). |
| Second Fundamental Theorem of Calculus (Fundamental Theorem of Calculus Part 2) | If F is an antiderivative of f, then \int_{a}^{b} f(x)dx = F(b) – F(a). |
| Continuous Function | A function without breaks or jumps on the specified interval. |
| Definite Integral | The value \int_{a}^{b} f(x)dx, representing net area under f(x) between x=a and x=b. |
Conclusion
In summary, the second fundamental theorem of calculus simplifies definite integrals by linking them to the evaluation of an antiderivative at boundary points. Because the fundamental theorem of calculus part 2 spares students from dealing with tedious sums, it is one of the most valuable tools in a calculus toolkit. Practicing how to choose correct antiderivatives and applying the theorem to real-world situations will strengthen understanding of both continuity and accumulation.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








