Differential equations are prominent in AP® Calculus AB-BC because they reveal how quantities change in relation to each other. One essential method for solving certain types of differential equations is called separation of variables. This technique focuses on separating an equation into parts that depend on x and y independently. Identifying when a differential equation is separable or non separable is vital for selecting the right approach.
Separable differential equations make solving more straightforward, while non separable differential equations often require alternative techniques. Understanding how to tell if a differential equation is separable helps with efficiently applying this method and avoiding unnecessary complications.
What We Review
Understanding Separable Differential Equations
What Does “Separable” Mean?
A separable differential equation allows the terms that involve y to stand on one side of the equality, and all x terms to stand on the other. Typically, a separable differential equation takes the form:
\frac{dy}{dx} = f(x) g(y)To see how to tell if a differential equation is separable, first check if the right-hand side or left-hand side can be factored into a function of x multiplied by a function of y. If such a factorization is possible, then it is likely a candidate for separation of variables.
Why Some Equations Are Non Separable
Many differential equations cannot be expressed in the form f(x) g(y). For instance, an equation like \frac{dy}{dx} = x + y cannot be cleanly factored into parts depending exclusively on x and exclusively on y. These non separable differential equations often require different solution methods, such as an integrating factor or other advanced techniques.
The Separation of Variables Technique
Step-by-Step Process
- Recognize a separable form. Look for an equation that can appear as \frac{dy}{dx} = f(x) g(y).
- Rearrange so that all y-terms multiply or divide on one side, and all x-terms multiply or divide on the other side.
- Integrate both sides with respect to their respective variables.
- Include the constant of integration, C, after integration.
- Solve for y in terms of x if possible, to obtain the explicit solution.
Example 1 with Full Walkthrough
Consider the differential equation:
\frac{dy}{dx} = x y^2Step-by-Step Solution
- Recognize it as separable. Notice that x y^2 is a product of a function of x (namely x) and a function of y (namely y^2).
- Separate the variables:
- \frac{1}{y^2} dy = x dx
- Integrate both sides:
- Left side: \int \frac{1}{y^2} dy = \int y^{-2} dy
- Right side: \int x dx
- Perform the integrations:
- Left side: \int y^{-2} dy = -y^{-1} + C_1
- Right side: \int x dx = \frac{x^2}{2} + C_2
- Combine the constants:
- -\frac{1}{y} = \frac{x^2}{2} + C (Where C represents C_2 - C_1.)
- Solve for y:
- -\frac{1}{y} = \frac{x^2}{2} + C \rightarrow\frac{1}{y} = -\left(\frac{x^2}{2} + C\right)
- y = \frac{-1}{\frac{x^2}{2} + C}
Graphing a slope field for the differential equation and drawing a few of its possible solutions can give you an idea of how the general solutions relate to the differential equation.
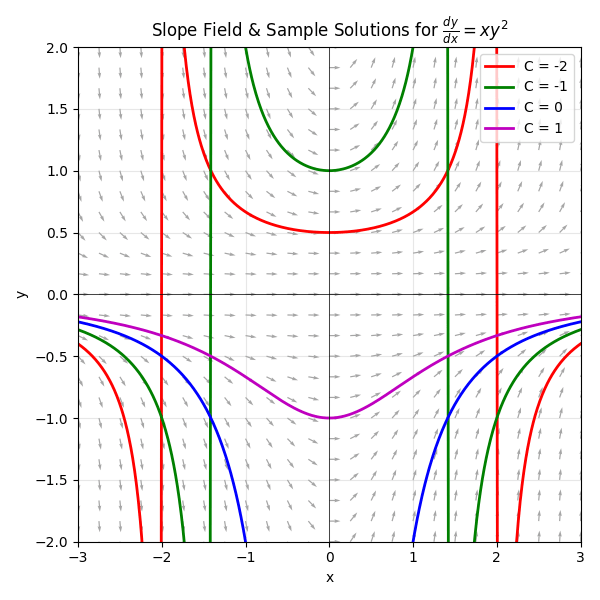
This result demonstrates how separation of variables provides a direct path from the differential equation to the explicit solution.
Additional Example
Example 2: Variation in Approach
Consider a second separable differential equation:
\frac{dy}{dx} = e^{x} \sin(y)Step-by-Step Solution
- Identify it as separable because it can be written as:
- f(x)g(y) = e^{x} \sin(y).
- Separate the variables:
- \frac{1}{\sin(y)} dy = e^{x} dx
- Integrate both sides:
- Left side: \int \frac{1}{\sin(y)} dy
- Right side: \int e^{x} dx
- Recall that \int \frac{1}{\sin(y)} dy = \ln|\tan(\frac{y}{2})| + C_1 (a known integral). Meanwhile, \int e^{x} dx = e^{x} + C_2.
- Combine the constants:
- \ln|\tan(\frac{y}{2})| = e^{x} + C
- Exponentiate both sides to solve for \tan(\frac{y}{2}):
- |\tan(\frac{y}{2})| = e^{e^{x} + C} = e^{C} e^{e^{x}}
- Since e^{C} is just another constant, label it as k.
- Then: \tan\left(\frac{y}{2}\right) = \pm k e^{e^{x}}
- Finally, y can be expressed by taking \frac{y}{2} = \tan^{-1}(\pm k e^{e^{x}}), though the exact form depends on boundary or initial conditions.
This example underscores how subtle differences in the integrand can affect the final expression.
Further Applications and Tips
- Separation might be tricky when factors are not obviously grouped. Carefully factor out functions to confirm if the equation is truly separable.
- Always check for extraneous values, especially those that make denominators zero or that might invalidate certain steps.
- In complex expressions, consider substitution if direct separation is not apparent. However, if the equation remains stubbornly mixed, it may be one of those non separable differential equations that require a different approach entirely.
Quick Reference Chart (Important Terminology and Definitions)
| Term | Definition |
| Separable Differential Equation | An equation in which the variables x and y can be separated onto opposite sides of the equality sign |
| Non Separable Differential Equation | An equation that cannot be rearranged into separate x and y functions |
| Antidifferentiation | The process of finding the indefinite integral |
| Constant of Integration (C) | The arbitrary constant added when integrating both sides |
Conclusion
Separation of variables simplifies certain differential equations by splitting x and y into distinct functions. Recognizing separable differential equations is crucial for solving them efficiently, while non separable differential equations require other methods. This procedure, tested frequently in AP® Calculus AB-BC, reveals patterns and helps predict the behavior of many real-life systems. Practice identifying how to tell if a differential equation is separable early on, as it will save time on exams and reinforce understanding of fundamental calculus concepts.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








