Nonlinear equations​ pop up on almost every SAT® Math section because they measure deeper algebra skills. Therefore, mastering them can boost scores quickly. This guide explains how to solve various nonlinear equations​ in one variable, highlights common pitfalls, and provides a handy vocabulary chart. Short examples, step-by-step solutions, and practice problems appear in every section so that concepts stay clear and memorable.

Quick Preview: What Counts as “Nonlinear Equations​”?

On the SAT®, an equation is nonlinear if its graph is not a straight line. Typical categories include

• Quadratic
• Radical (variables inside a root sign)
• Rational (variables in the denominator)
• Absolute value
• Higher-degree polynomial (cubic, quartic, etc.)

Sometimes, a system combines a line with one of these nonlinear types. Those mixed systems also appear often.

Quadratic Equations—The SAT®’s Favorite

Spotting a Quadratic

A quadratic is any equation that can be rearranged into:

ax^2+bx+c=0

…where a \neq 0.

It may first show up in factored form, vertex form, or even hidden inside fractions.

Method 1: Factoring

Example

Solve x^2-5x+6=0.

Step 1: Look for two numbers that multiply to 6 and add to −5.

Those numbers are −2 and −3.

Step 2: Rewrite as factors.

x-2(x-3)=0

Step 3: Apply the Zero Product Property by setting each factor equal to zero.

x-2=0 or x-3=0

Step 4: Solve.

x=2 or x=3

Practice Problem

Solve x^2+2x-15=0 by factoring.

Method 2: Completing the Square

Example

Solve x^2+6x-7=0.

Step 1: Move the constant.

x^2+6x=7

Step 2: Take half of 6 (3), square it (9), then add to both sides.

x^2+6x+9=7+9

Step 3: Write the left side as a perfect square.

x^2=16

Step 4: Take square roots.

x+3=\pm4

Step 5: Solve both cases.

x=1 or x=-7

Practice Problem

Solve x^2-4x+1=0 by completing the square.

Method 3: Quadratic Formula & Discriminant

The formula always works, even when factoring is messy.

Quadratic Formula:

x=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}

Discriminant

D=b^{2}-4ac

• If D>0, two real solutions
• If D=0, one real solution
• If D<0, no real solutions (complex)

Example

Solve 3x^{2}+2x-1=0.

Step 1: Identify coefficients: a=3, b=2, c=-1.

Step 2: Compute D=2^{2}-4(3)(-1)=4+12=16. Therefore, two solutions exist.

Step 3: Substitute into the formula.

x=\dfrac{-2\pm\sqrt{16}}{6}=\dfrac{-2\pm4}{6}

Step 4: Separate the cases.

x=\dfrac{2}{6}= \dfrac{1}{3} or x=\dfrac{-6}{6}=-1.

Practice Problem

Use the quadratic formula to solve 2x^{2}-7x+3=0.

Mini-Tip Box

• Standard form helps the quadratic formula work smoothly.
• Vertex form a(x-h)^{2}+k=0 makes completing the square almost instant. Therefore, rewrite equations if it saves time.

Radical Equations—Watch for Extraneous Roots

General Plan

1. Isolate the radical.
2. Square both sides.
3. Solve, then check every answer in the original equation. Extraneous roots often appear because squaring hides sign information.

Example

Solve \sqrt{2x-1}=x-3.

Step 1: Square both sides.

2x-1=(x-3)^{2}

Step 2: Expand and collect terms.

2x-1=x^{2}-6x+90=x^{2}-8x+10

Step 3: Use the quadratic formula.

x=\dfrac{8\pm\sqrt{64-40}}{2}= \dfrac{8\pm\sqrt{24}}{2}=4\pm\sqrt{6}

Step 4: Check the solutions to the original problem.

Only x=4+\sqrt{6}\approx6.45 keeps the left side positive. The smaller root is extraneous.

Practice Problem

Solve and check \sqrt{x+4}=x-2.

Rational Equations—Clear Those Denominators

Procedure

1. Identify the least common denominator (LCD).
2. Multiply every term by the LCD to eliminate fractions.
3. Solve the resulting polynomial equation.
4. Exclude any values that make the denominator zero.

Example

Solve \dfrac{3}{x}+\dfrac{2}{x-1}=1.

Step 1: The LCD is x(x-1).

Step 2: Multiply:

3(x-1)+2x= x(x-1)

3x-3+2x= x^{2}-x

Step 3: Rearrange.

0=x^{2}-6x+3

Step 4: The quadratic formula gives:

x=\dfrac{6\pm\sqrt{36-12}}{2}=3\pm\sqrt{6}

Step 5: Both values are allowed because neither makes the denominator zero.

Practice Problem

Solve \dfrac{5}{x+2}-\dfrac{1}{x}=1 and state any excluded values.

Absolute Value Equations—Two Cases, One Strategy

The absolute value measures distance from zero, so it is never negative.

To solve |A|=B:

• If B<0, no solution.
• Otherwise split into A=B and A=-B.

Example

Solve |3x-7|=5.

Case 1: 3x-7=5 → x=4

Case 2: 3x-7=-5 → x=\dfrac{2}{3}

Practice Problem

Solve |2x+1|=4.

Polynomial Equations in Factored Form—Zero Product Property

If the test already provides a factored polynomial, life is easy.

Example

Solve (x+4)(2x-3)(x-1)=0.

Set each factor to zero:

x=-4, x=\dfrac{3}{2}, or x=1

Practice Problem

Solve x(x-5)(x+2)=0.

Systems That Mix Linear and Nonlinear Equations​

Substitution is usually fastest because one equation is linear.

Example

Solve the system:

\begin{cases} y=2x+1 \\ y=x^{2}-4x+5 \end{cases}

Step 1: Substitute the linear expression for y.

2x+1=x^{2}-4x+5

Step 2: Rearrange.

0=x^{2}-6x+4

Step 3: Discriminant check.

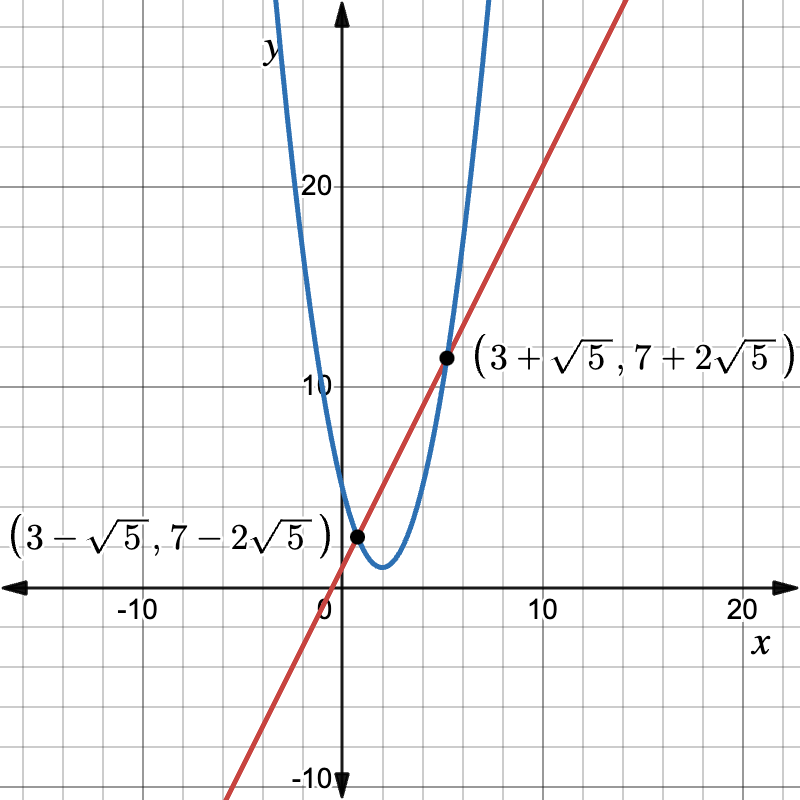
D=(-6)^{2}-16=20>0, so two intersection points exist.

Step 4: Solve with the quadratic formula.

x=\dfrac{6\pm\sqrt{20}}{2}=3\pm\sqrt{5}

Step 5: Solve for y using y=2x+1. Therefore, the solutions are:

\bigl(3+\sqrt{5},\ 7+2\sqrt{5}\bigr) and \bigl(3-\sqrt{5},\ 7-2\sqrt{5}\bigr)

Graphically, these are the points of intersection of the two functions.

Practice Problem

Solve the system and state the number of real intersections.

\begin{cases}y=-x+6 \\ y=x^{2}-4 \end{cases}

Interpreting Solutions in Word Problems

SAT® word problems often hide quadratics inside motion or revenue formulas. Consequently, interpreting roots matters.

Example

A projectile is launched so that its height in meters after t seconds is:

h(t)=-5t^{2}+20t+3

When does it hit the ground?

Set the height to zero.

-5t^{2}+20t+3=0 → divide by −1.

5t^{2}-20t-3=0

The quadratic formula yields t=\dfrac{20\pm\sqrt{400+60}}{10}= \dfrac{20\pm\sqrt{460}}{10}.

The negative time is discarded, so the positive root gives the landing time.

Quick Reference Vocabulary Chart

Term	Concise Definition	SAT® Tip
Quadratic	Equation with the highest power of 2	Usually solvable by factoring or formula
Discriminant	b^{2}-4ac	Tells the number of real roots quickly
Extraneous Solution	Root that fits the transformed equation but not the original	Always check radical or rational answers
LCD (Least Common Denominator)	Smallest expression that includes every denominator factor	Clears fractions in one step
Zero-Product Property	If AB=0, then A=0 or B=0	Key for factored polynomials
Parameter	A constant that can vary between problems	Treat fixed values as numbers during solving
Vertex Form	a(x-h)^{2}+k	Helpful for completing the square

Final Checklist & Practice Reminders

• Identify the equation type first; structure guides the quickest method.
• Clear denominators or radicals before solving.
• Use the discriminant to predict the number of quadratic solutions.
• Always test for extraneous roots.
• Practice under timed conditions to mimic the SAT® pace.

Explore additional SAT® Math practice sets on nonlinear equations​ for targeted drills and steady score growth.

Answers to Practice Problems

1. Quadratic factoring: x=-5 or x=3.
2. Completing the square: x=2\pm\sqrt{3}.
3. Quadratic formula: x=\dfrac{7\pm\sqrt{13}}{4}.
4. Radical check: x=4.
5. Rational: excluded x=-2,0; solutions x=1 or x=-3.
6. Absolute value: x=\dfrac{3}{2} or x=-\dfrac{5}{2}.
7. Factored polynomial: x=0,5,-2.

With these tools and regular practice, solving nonlinear equations​ on the SAT® becomes manageable and even enjoyable. Good luck on test day!

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.