What We Review
Introduction
The squeeze theorem, also called the sandwich theorem, is a valuable tool for solving limit problems in AP® Calculus AB-BC. It helps establish the value a function approaches by “squeezing” it between two simpler functions. Squeeze theorem examples illustrate this concept and are closely related to the limit concept from LIM-1.E.2, where limits can be confirmed by bounding one function between two others that share the same limit.
Students often encounter complicated expressions, especially when working on trigonometric and polynomial limits. Therefore, understanding the squeeze theorem is key. It simplifies these problems and ensures consistent results.
Understanding the Squeeze Theorem
Definition
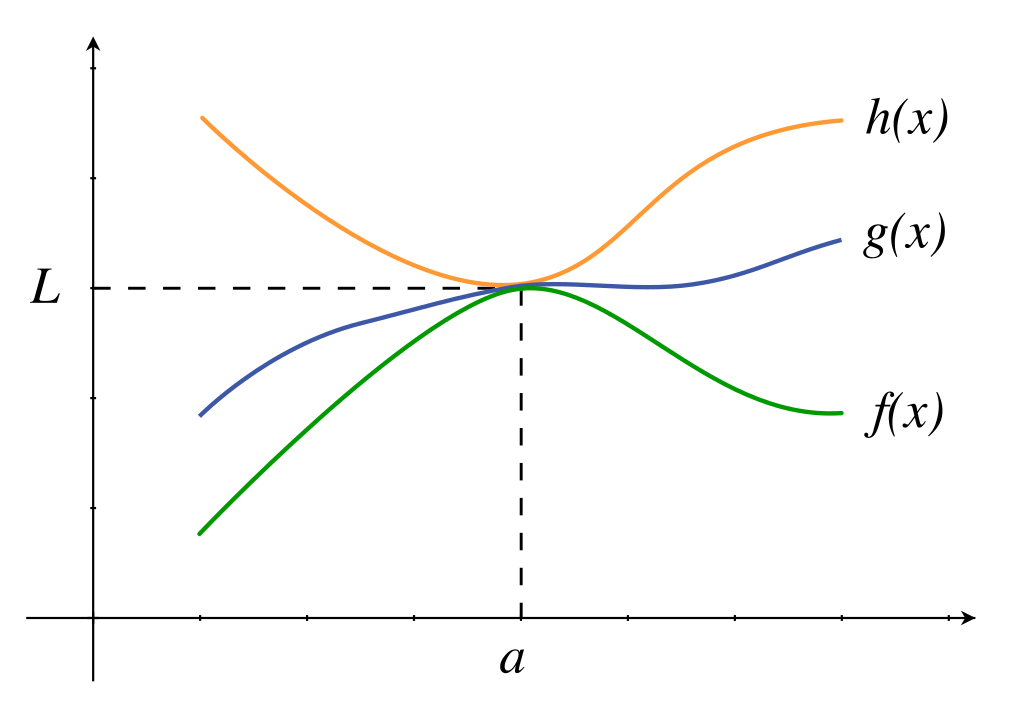
The squeeze theorem states: if one function is always less than or equal to a second function, which in turn is less than or equal to a third function, and the first and third functions share the same limit, then the middle function must have that same limit. In mathematical terms, assume functions f(x), g(x), and h(x) satisfy:f(x) \le g(x) \le h(x) and \lim_{x \to a} f(x) = \lim_{x \to a} h(x) = L. Then the theorem guarantees: \lim_{x \to a} g(x) = L.
This result is possible only if the inequalities hold in a neighborhood around the point (except possibly at the point itself).
Why It Works
The core idea is simple. If both bounding functions agree to approach the same value as x approaches a, any function squeezed between them has nowhere else to go but to the same limit. This approach is especially helpful for tricky limit problems that do not simplify using standard algebra. The squeeze theorem adds a useful tool to the AP® Calculus AB-BC toolkit because it handles limits that involve indeterminate behavior, complicated trigonometric expressions, or oscillating functions.
Applying the Squeeze Theorem Step by Step
- Identify a function that needs a limit evaluation.
- Find suitable bounding functions that are simpler to handle.
- Verify that f(x) \le g(x) \le h(x) (or the reversed inequality).
- Confirm that \lim_{x \to a} f(x) and \lim_{x \to a} h(x) exist and are equal.
- Conclude that \lim_{x \to a} g(x) must be the same as those shared limits.
These steps ensure that the final result does not rely on guesswork. Therefore, the squeeze theorem confirms the limit logically.
Squeeze Theorem Examples
Example 1: Trigonometric Limit
Consider \lim_{x \to 0} x \sin\bigl(\tfrac{1}{x}\bigr).
1. Setup
Notice that \sin\bigl(\tfrac{1}{x}\bigr) oscillates between -1 and 1. Therefore, the product x \sin\bigl(\tfrac{1}{x}\bigr) stays between -|x| and |x|.
2. Work Through the Inequality
Since -1 \le \sin\bigl(\tfrac{1}{x}\bigr) \le 1, multiply everything by x (and note the sign of x when x \to 0):-|x| \le x \sin\bigl(\tfrac{1}{x}\bigr) \le |x|.
3. Find the Limit
Observe that \lim_{x \to 0} -|x| = 0 and \lim_{x \to 0} |x| = 0. Because both bounding functions share the same limit of 0, the squeeze theorem tells us:\lim_{x \to 0} x \sin\bigl(\tfrac{1}{x}\bigr) = 0.
Practice Problem
Find \lim_{x \to 0} x^2 \sin\bigl(\tfrac{1}{x}\bigr).Solution Steps:
- Note that -1 \le \sin\bigl(\tfrac{1}{x}\bigr) \le 1.
- Multiply by x^2 to get -x^2 \le x^2 \sin\bigl(\tfrac{1}{x}\bigr) \le x^2.
- The limit of -x^2 and x^2 as x \to 0 is 0.
- By the squeeze theorem, \lim_{x \to 0} x^2 \sin\bigl(\tfrac{1}{x}\bigr) = 0.
Example 2: Algebraic/Polynomial Limit
Consider \lim_{x \to 0} \frac{x^2}{2} while comparing it to nearby functions. Although this may look straightforward, it demonstrates the setup clearly.
1. Setup
Suppose one needs to show a limit in a similarly structured scenario, such as proving \frac{x^2}{2} is bounded by two functions that share the same limit.
2. Demonstrate Steps
- Choose bounding functions: 0 \le \frac{x^2}{2} \le x^2 for x \ge 0.
- Notice \lim_{x \to 0} 0 = 0 and \lim_{x \to 0} x^2 = 0.
- Squeeze \frac{x^2}{2} between 0 and x^2.
3. Conclude the Limit Result
Since both bounding functions go to 0, the function in between must go to 0. Thus, \lim_{x \to 0} \frac{x^2}{2} = 0.
Practice Problem
Determine \lim_{x \to 0} x^4 by squeezing it between two suitable bounds. Solution Steps:
- Recognize that 0 \le x^4 \le x^2 for |x| \le 1.
- Know that \lim_{x \to 0} 0 = 0 and \lim_{x \to 0} x^2 = 0.
- Conclude by the squeeze theorem that \lim_{x \to 0} x^4 = 0.
Key Insights and Tips
- The squeeze theorem proves especially useful when dealing with trigonometric functions that oscillate.
- When a function seems unmanageable by direct substitution, consider whether upper and lower bounding functions exist.
- Checking behavior near zero often reveals absolute value inequalities like -|f(x)| \le f(x) \le |f(x)|.
- This theorem frequently appears in AP® Calculus AB-BC contexts, making it a vital resource for exam success.
Quick Reference Chart of Important Terms and Definitions
| Vocabulary | Definition |
| Squeeze Theorem | A theorem stating that if f(x) ≤ g(x) ≤ h(x)… and f, h share the same limit L, then g must also have limit L. |
| Limit | The value a function approaches as the input moves toward a certain point. |
| Bounding Function | A simpler function acting as an upper or lower limit for another function. |
| Oscillation | Repeated swinging between extremes, as with sin(1/x). |
Conclusion
The squeeze theorem offers a powerful strategy for evaluating limits, where direct methods might fail. By finding bounding functions that share the same limit, it becomes straightforward to show that a complicated function’s limit must match. This skill is essential in AP® Calculus AB-BC, as proven limit shortcuts can simplify exam questions significantly. Mastering the squeeze theorem strengthens overall understanding of limit behavior and fosters confidence during challenging limit problems, reinforcing a deeper grasp of calculus fundamentals.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








