Introduction

Systems of linear equations show up in nearly every SAT® Math section. Therefore, understanding the system of linear equations is a high-value skill for raising your score. This guide explains how to create, solve, and interpret two-variable systems with ease. Along the way, you will learn how to move among tables, equations, and graphs while spotting whether a system has a unique solution, no solution, or infinitely many solutions. By the end, solving linear systems will feel routine instead of risky.

The Building Blocks: A Single Linear Equation

Before handling two equations, let’s review one.

• Variable – the unknown number
• Coefficient – the number in front of the variable
• Constant – the stand-alone number
• Term – each separate “piece” joined by plus or minus signs

Most SAT® items present lines in slope-intercept form, y = mx + b. Here, m is slope and b is the y-intercept.

Mini Example

Graph y = 2x + 3.

1. Intercept: Plot (0, 3).
2. Slope: rise 2, run 1 to reach (1, 5).
3. Draw the line through both points.

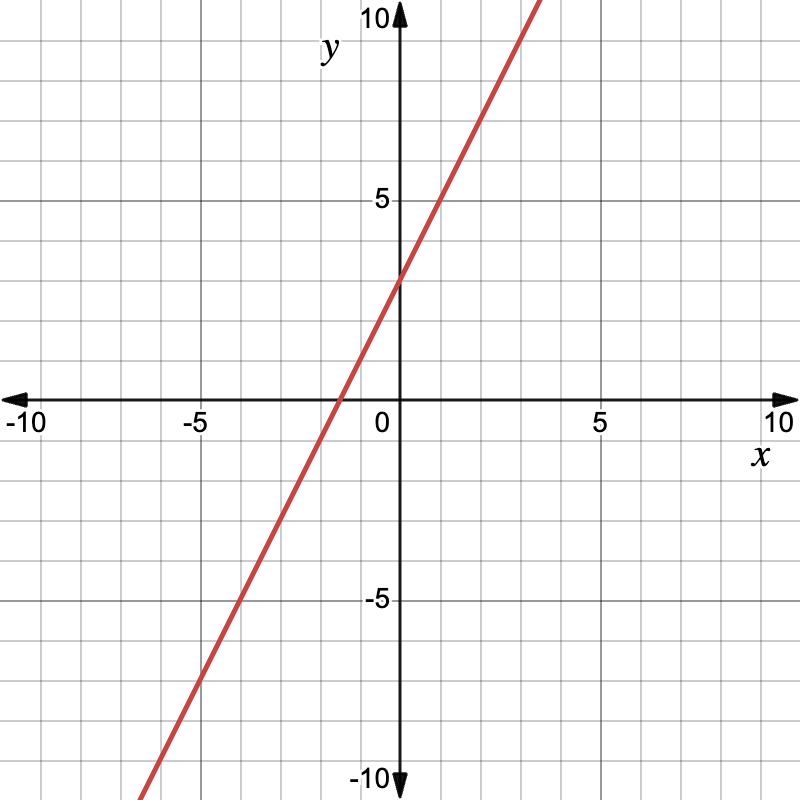
A single line is nice, but two lines working together can solve real SAT® problems in seconds.

Turning Words into Math: Creating a System from Real-World Context

Translating plain language into algebra is a core SAT® skill. Common contexts include mixtures, money, motion, and geometry.

Example: Concert Tickets

Student tickets cost \$6 each, and adult tickets cost \$10 each. A club sells 40 tickets for \$320. How many of each type were sold?

1. Define variables
   • x = number of student tickets
   • y = number of adult tickets
2. Write the equations
   • Quantity: x + y = 40
   • Money: 6x + 10y = 320
3. Note on interpretation
   • Solving will give an ordered pair (x, y). That pair must make sense—negative tickets are impossible.

Three Ways to View the Same System

Seeing a system three different ways helps you work faster.

1. Tabular – a table of values
2. Algebraic – two equations
3. Graphical – two lines on the coordinate plane

Example

Table:

x	y
0	4
2	0

x	y
0	–1
4	1

Convert each row set into slope-intercept form.

First line:

The slope is \dfrac{0 – 4}{2 – 0} = –2. So y = -2x + 4.

Second line:

The slope is \dfrac{1 – (–1)}{4 – 0} = 0.5. So y = 0.5x - 1.

Graph both lines. They intersect at (2, 0).

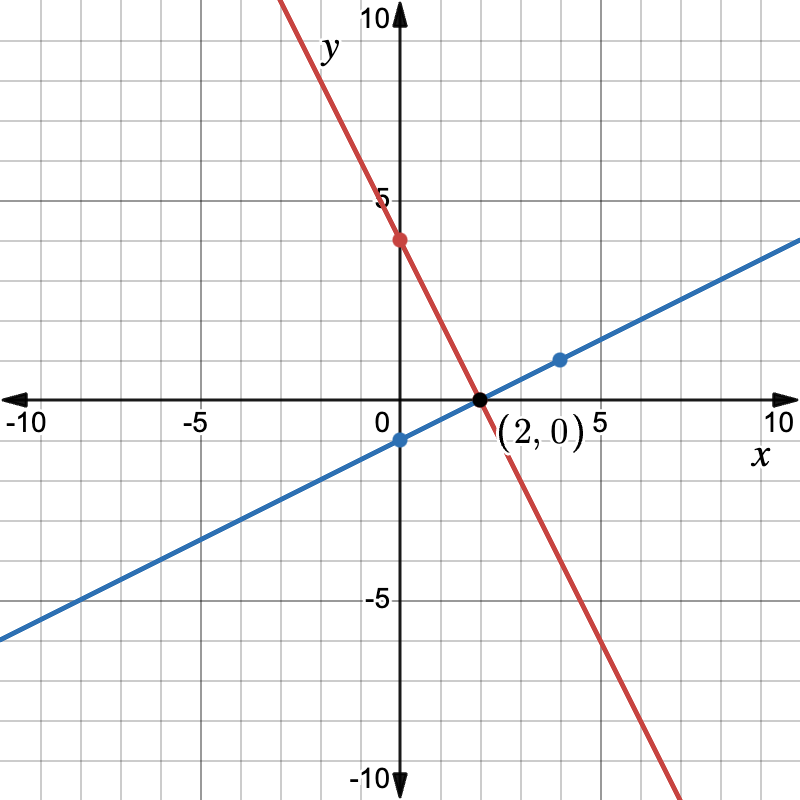
Move easily from table → equation → graph to confirm answers.

Solving Systems Efficiently

A. Graphing Method

Pros: visual, quick estimate.

Cons: exact answers hard if intersection is off-grid.

Example: Solve \begin{cases} y = -x + 6 \\ y = 2x - 3 \end{cases} by graphing.

1. Plot the y-intercepts (0, 6) and (0, –3).
2. Draw both lines. They intersect at (3, 3).
3. Therefore, the unique solution is (3, 3).

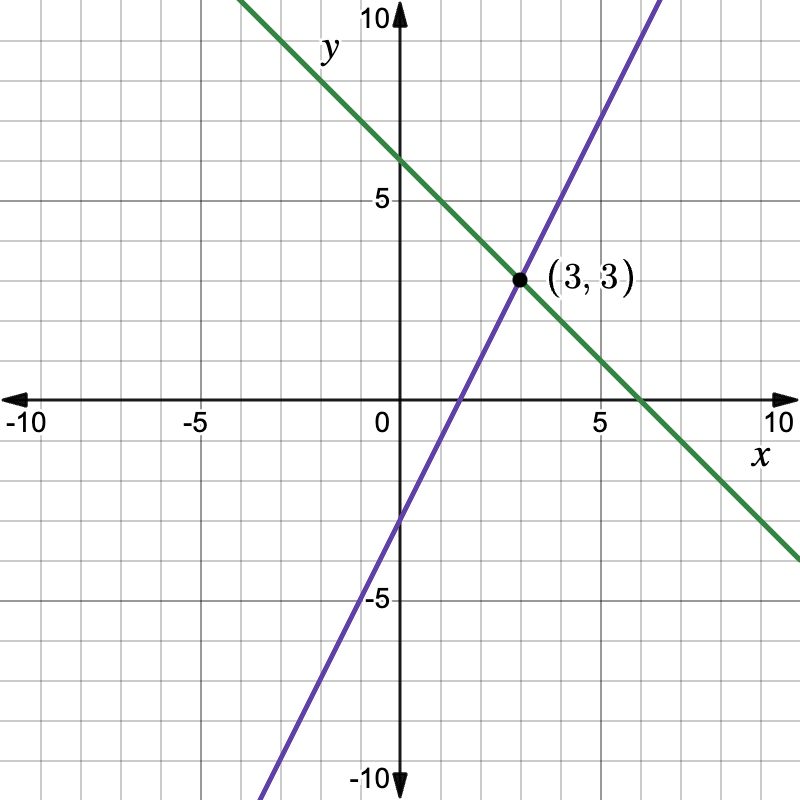
B. Substitution Method

Best when one equation is solved for a variable.

Example: Solve \begin{cases} y = 4x - 1 \\ 2x + 3y = 17 \end{cases}

Step	Reason
2x + 3(4x - 1) = 17	Substitute 4x - 1 for y
2x + 12x - 3 = 17	Distribute 3 to both terms
14x = 20	Combine like terms and add 3 to both sides
x = \dfrac{10}{7}	Divide both sides by 14
y = 4\left(\dfrac{10}{7}\right) - 1 = \dfrac{40}{7} - 1 = \dfrac{33}{7}	Substitute x into the equation for y
\left(\dfrac{10}{7}, \dfrac{33}{7}\right)	Final solution ✅

C. Elimination Method

Ideal when the coefficients line up.

Example: Solve \begin{cases} 3x + 2y = 16 \\ 5x - 2y = 4 \end{cases}

Step	Reason
(3x + 2y) + (5x - 2y) = 16 + 4	Add both equations to eliminate y
8x = 20	Combine like terms
x = 2.5	Divide both sides by 8
3(2.5) + 2y = 16	Substitute x = 2.5 into the first equation
7.5 + 2y = 16	Multiply
2y = 8.5	Subtract 7.5 from both sides
y = 4.25	Divide both sides by 2
(2.5, 4.25)	Final solution ✅

D. Choosing the Best Method—Decision Checklist

• If coefficients already match, use elimination.
• If a variable is isolated, use substitution.
• If both intercepts are integers and the grid is given, quick-sketch graphing can suffice.
• Under time pressure, scan for mental-math cancellations first.

Solution Conditions: One, None, or Infinitely Many?

• Unique solution – lines intersect once; slopes different.
• No solution – lines are parallel; slopes equal but intercepts differ.
• Infinitely many – lines coincide; both slope and intercept match.

Quick slope test: put each equation into slope-intercept form. Compare m and b.

Example

Classify without solving.

a) \begin{cases} 4x - 2y = 8 \\ 2x - y = 4 \end{cases}

First, divide the first equation by 2: 2x - y = 4. This is the same as the second equation. Therefore, there are infinitely many solutions.

b) \begin{cases} y = 3x + 1 \\ 6x - 2y = 5 \end{cases}

Rearrange the second equation: -2y = -6x + 5 → y = 3x - 2.5. The slopes of both equations are equal, but their y-intercepts differ. So, there are no solutions.

c) \begin{cases} y = -0.5x + 7 \\ y = 2x - 1 \end{cases}

The slopes of both equations are different. Therefore, there is one solution.

Bringing the Algebra Back to the Story

After computing (x, y), always ask, “What does this pair mean?”

Example: Geometry Perimeter

A rectangle’s perimeter is 26 cm. Its length exceeds its width by 3 cm. Find its dimensions.

Variables: w = width, l = length

Equations:

\begin{cases} l = w + 3 \\ 2l + 2w = 26 \end{cases}

One variable is isolated, so we can use substitution to solve.

Step	Reason
2(w + 3) + 2w = 26	Substitute w+3 into the second equation
2w + 6 + 2w = 26	Distribute 2 into parentheses
4w + 6 = 26	Combine like terms
4w = 20	Subtract 6 from both sides
w = 5	Divide both sides by 4

If the width is 5 cm, the length is 5+3=8 cm.

Check for extras: negative lengths would be rejected.

Common SAT® Traps & Time-Saving Tips

• Misaligned variables – double-check that x pairs with x, y with y.
• Disguised like terms – 0.5x equals \frac{x}{2}; rewrite to match.
• Off-grid intersections – if slopes differ but intercepts are difficult to read, switch from graphing to elimination.
• Mental-math elimination – add 7x and –7x mentally to cancel before writing.
• Bubble strategy – for grid-ins, always reduce fractions like \frac{6}{8}to \frac{3}{4} to avoid scoring machines misreading.

IX. Quick-Reference Vocabulary Chart

Term	Simple Definition	SAT® Tip
Variable	A symbol (x or y) that stands for an unknown number	Label units to avoid mix-ups
Coefficient	Number that multiplies the variable	Watch the sign (+/–)
Constant	Fixed number with no variable attached	Often moves when rearranging
System of Linear Equations	Two equations using the same variables	On SAT®, almost always two variables
Solution to a System	An (x, y) pair that makes BOTH equations true	The point where the lines meet
Elimination Method	Add or subtract equations to cancel a variable	Align like terms first

Final Takeaways & Next Steps

Systems of linear equations power many SAT® Math questions. Master the core steps: create equations from words, represent them in multiple ways, solve efficiently, and interpret answers. Therefore, practice timed drills to lock in speed. For more targeted practice, explore additional SAT® math questions and track accuracy. Confidence grows with each solved system.

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.