Circle questions pop up all over the SAT® Math section. However, many students lose points simply because they mix up degrees and radians or forget a key fact about the unit circle​. Therefore, this guide breaks everything into bite-sized pieces so that converting angles, finding arc lengths, and writing circle equations becomes automatic.

Focus keywords woven throughout: degrees, radians, unit circle, circle equation, SAT® Math.

Why Degrees, Radians, and the Unit Circle Matter on the SAT®

• Roughly 15–20\% of SAT® Math questions involve circles, angles, or trigonometry.
• Mastering degrees and radians speeds up arc-length and sector-area problems.
• Knowing unit-circle coordinates makes sine, cosine, and tangent questions almost free points.

Circle Vocabulary Crash Course

Key Parts of a Circle

• Radius: Segment from the center to any point on the circle.
• Diameter: Longest chord; equals two radii.
• Chord: Any segment with endpoints on the circle.
• Tangent: A line touching the circle at exactly one point.
• Secant: A line that cuts the circle twice.
• Central Angle: Angle with its vertex at the center.
• Arc: Curved part of the circumference.

Quick Illustration

Imagine a pizza. The crust is the circumference, a slice’s tip is the center, and the cheese edge of one slice is an arc.

Example Problem

A circle has center at O. Point A lies on the circle. Line AB touches the circle only at A. Segment AC goes through the circle and exits at D. Identify each part:

Solution

1. \overline{OA} joins center O to point A ⇒ radius.
2. \overline{AB} touches at one point ⇒ tangent.
3. \overline{AD} or \overline{AC} (extended) cuts twice ⇒ secant.

Converting Between Degrees and Radians

Core Formula & Proportion

\pi \text{ rad} = 180^\circ

Therefore,

\dfrac{\text{radians}}{\pi} = \dfrac{\text{degrees}}{180}

Example

a) Convert 135^\circ to radians.

Start with the proportion:

\dfrac{x}{\pi} = \dfrac{135}{180}

Simplify the right side:

\dfrac{135}{180} = \dfrac{3}{4}

Now multiply both sides by \pi:

x = \dfrac{3\pi}{4} radians

b) Convert \frac{5\pi}{6} to degrees.

Start with the proportion:

\dfrac{5\pi/6}{\pi} = \dfrac{d}{180}

Simplify the left side:

\dfrac{5\pi}{6\pi} = \dfrac{5}{6}

Cross-multiply to solve for d:

d = 180 \times \dfrac{5}{6} = 150^\circ

Mini Practice

Convert quickly (answers underneath):

1. 300^\circ → ? rad
2. \frac{\pi}{3} → ? °
3. \frac{7\pi}{4} → ? °

Answers:

1. \frac{5\pi}{3} rad
2. 60^\circ
3. 315^\circ

Meet the Unit Circle

Definition

The unit circle is a circle with a radius of 1 centered at the origin. Because the radius is 1, the coordinate of any point P tells you the cosine and sine directly:P(\cos\theta,\sin\theta)

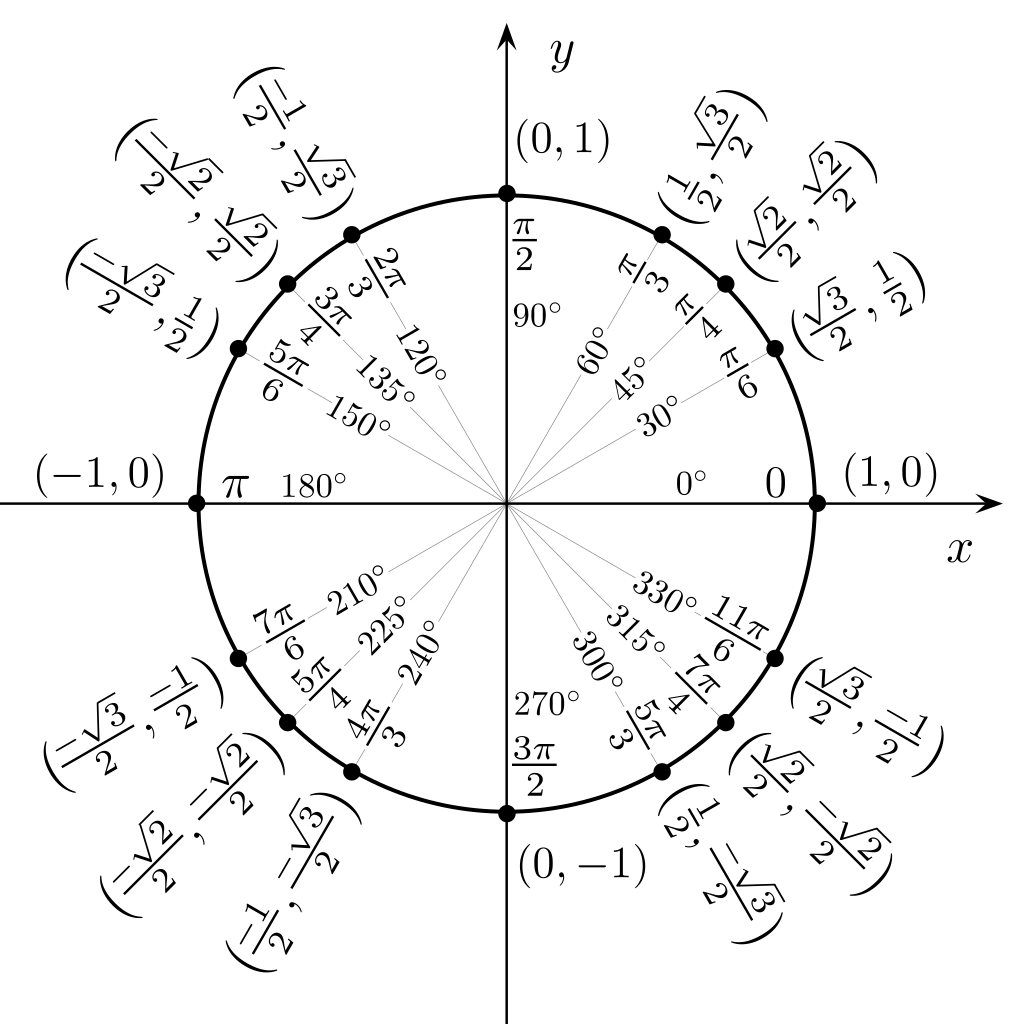
Quadrants and Symmetry

Angles start at the positive x-axis and move counter-clockwise:

• Quadrant I: 0°^\circ–90^\circ (all trig ratios are positive)
• Quadrant II: 90^\circ–180^\circ
• Quadrant III: 180^\circ–270^\circ
• Quadrant IV: 270^\circ–360^\circ

However, symmetry means you can find one coordinate and mirror it.

Must-Know Angle Coordinates

Angle	Coordinate (x, y)
0^\circ	(1, 0)
30^\circ	\left( \dfrac{\sqrt{3}}{2} , \dfrac{1}{2}\right )
45^\circ	\left( \dfrac{\sqrt{2}}{2} , \dfrac{\sqrt{2}}{2} \right)
60^\circ	\left( \dfrac{1}{2} , \dfrac{\sqrt{3}}{2} \right)
90^\circ	(0, 1)

Likewise, reflect signs for other quadrants.

Memory Tricks

• Special triangles: 45-45-90 and 30-60-90.
• The phrase “All Students Take Calculus” tells which trig ratios are positive in each quadrant.
  • Quadrant I: All trig functions
  • Quadrant II: Only sine
  • Quadrant III: Only tangent
  • Quadrant IV: Only cosine

Example Problem

Find \sin 150^\circ using the unit circle.

Solution

1. Notice 150^\circ is in Quadrant II.
2. Reference angle = 180^\circ − 150^\circ = 30^\circ.
3. In Quadrant II, sine stays positive.
4. \sin 30^\circ = \frac{1}{2} ⇒ therefore, \sin 150^\circ = \frac{1}{2}.

Arc Length and Sector Area

Formulas in Radians

Given radius r and angle \theta (in radians):

Arc length: s = r\theta

Sector area: A = \frac{1}{2} r^2 \theta

Why Radians Are Cleaner

Notice that neither formula needs 180 or π when \theta is in radians. Degrees would force an extra conversion.

Example

A Ferris wheel has a radius of 40 m. It turns through \frac{\pi}{3} radians. Find:

Solution

a) s = 40 \times \frac{\pi}{3} = \frac{40\pi}{3}\ \text{m}

b) A = \frac{1}{2}\times 40^2 \times \frac{\pi}{3} = \frac{1}{2}\times 1600 \times \frac{\pi}{3}= \frac{800\pi}{3}\ \text{m}^2

Circle Equations in the Coordinate Plane

Standard Form

x-h^2 + (y-k)^2 = r^2 (h, k) = center, r = radius.

Connection to Unit Circle

The unit circle is simply the special case where (h, k) = (0, 0) and r = 1.

Example

Does point (4, −1) lie on x-2^2 + (y+1)^2 = 9?

Solution

1. Substitute x = 4, y = −1:
   • (4-2)^2 + (-1+1)^2 = 2^2 + 0^2 = 4
2. Right side is 4, but circle’s r^2 is 9. Therefore, the point is inside the circle, not on it.

Completing the Square to Reveal a Hidden Circle

General to Standard Form

Start with x^2 + y^2 + Dx + Ey + F = 0. Complete squares for both variables.

Example

Rewrite x^2 + y^2 - 6x + 4y + 9 = 0 and find center & radius.

Solution

1. Group: (x^2 - 6x) + (y^2 + 4y) = -9

2. Complete squares:

(x^2 - 6x + 9) + (y^2 + 4y + 4) = -9 + 9 + 4

• x part: take half of −6 ⇒ −3, square ⇒ 9.
• y part: half of 4 ⇒ 2, square ⇒ 4.

Add 9 and 4 to both sides.

3. Rewrite: x-3^2 + (y+2)^2 = 4

Therefore, the center is at (3, −2), radius \sqrt{4}=2.

Transformations: How Equation Changes Affect the Graph

Shifts

Moving x-h^2 + (y-k)^2 = r^2 right or left changes h; up or down changes k.

Dilation

Changing r scales the circle outward (larger r) or inward (smaller r).

Example

Original: x-1^2 + (y+2)^2 = 16. Move the circle 3 units up.

New k = −2 + 3 = 1. The equation becomes:

x-1^2 + (y-1)^2 = 16

Distance Formula: Verifying Points on a Circle

Formula Review

Distance between (x_1, y_1) and (x_2, y_2): \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Example

Show that (−2, 5) sits on a circle of radius \sqrt{29} centered at (1, 1).

Distance:

\sqrt{(-2-1)^2 + (5-1)^2} = \sqrt{(-3)^2 + 4^2} = \sqrt{9+16} = \sqrt{25}=5

Since 5 = \sqrt{25} \neq \sqrt{29}, the point is outside the circle.

Quick Reference Chart: Essential Vocabulary & Formulas

Term	Definition / Key Formula
Radian	Angle measure where arc length equals radius
Degree	\dfrac{1}{360} of a full rotation
Central Angle	Angle with vertex at the circle’s center
Arc	Curved segment of circumference
Arc Length	s = r\theta (\theta in radians)
Sector Area	A = \frac{1}{2}r^2\theta
Unit Circle	Circle with r = 1, center (0,0)
Standard Circle Equation	x-h^2 + (y-k)^2 = r^2
Completing the Square	Process to convert general → standard form
Reference Angle	Acute angle formed with x-axis
Tangent Line	Touches circle at one point
Secant Line	Intersects the circle at two points

SAT®-Style Practice Questions

1. Convert 210^\circ to radians.
2. Evaluate \cos\left(\frac{7\pi}{6}\right) using the unit circle.
3. Find the arc length of a circle with radius 6 cm subtended by 120^\circ.
4. Write the equation of a circle centered at (−4, 2) that passes through (−1, 2).
5. Complete the square: x^2 + y^2 + 2x - 8y = 23 and state the radius.

Solutions

1. \frac{7\pi}{6}
2. -\frac{\sqrt3}{2}
3. 4\pi\ \text{cm}
4. (x+4)^2 + (y-2)^2 = 9
5. Radius = 2\sqrt{10}

Final Tips & Takeaways

• Always convert degrees to radians before using s = r\theta or A = \frac12 r^2\theta; it prevents careless errors.
• Drill the five special angles (0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ) until their coordinates pop into mind instantly.
• When stuck on a general circle equation, remember: complete the square, then read off the center and radius.
• On test day, sketch mini diagrams; even five-second drawings reduce mistakes.

Master these concepts, and circle problems will feel like—well—a walk in the park rather than a spin in circles. Good luck on the SAT®!

Sharpen Your Skills for SAT® Math (Digital)

Are you preparing for the SAT® Math (Digital) test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world SAT® Math (Digital) problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your SAT® Math (Digital) exam?

Albert has hundreds of SAT® Math (Digital) practice questions, free response, and full-length practice tests to try out.