The Intermediate Value Theorem (IVT) is a fundamental concept in calculus courses, including AP® Calculus AB-BC. It ensures that if a continuous function changes from one value to another over a closed interval, it will take every value in between. This property is powerful for finding solutions to equations and understanding the behavior of functions. Continuity plays a central role because “breaks” or “jumps” in a function block the IVT from being valid.
What We Review
Understanding Continuity
Definition of a Continuous Function on a Closed Interval
A function f(x) is continuous on a closed interval [a, b] if it has no gaps or jumps for any x in [a, b]. In simpler terms, the function can be traced from x = a to x = b without lifting a pencil if it were drawn by hand.
For instance, a polynomial like f(x) = x^2 - 4 is continuous on every interval, including [-2, 2]. However, a function with a denominator that becomes zero at certain points is discontinuous at those points.
Why Continuity Matters
Continuity is crucial because the IVT requires the function to have no sudden jumps. Therefore, the IVT would not work for functions that are missing a point or have a break in the path. This theorem allows problem solvers to confirm that every value between f(a) and f(b) will appear for some c in [a, b].
What Is the Intermediate Value Theorem?
Formal Definition
The Intermediate Value Theorem can be stated as follows:
If f is continuous on a closed interval [a, b], and s is any number between f(a) and f(b), then there is at least one point c in [a, b] for which f(c) = s. The image below demonstrates three points where f(x) = s in the interval [a, b].
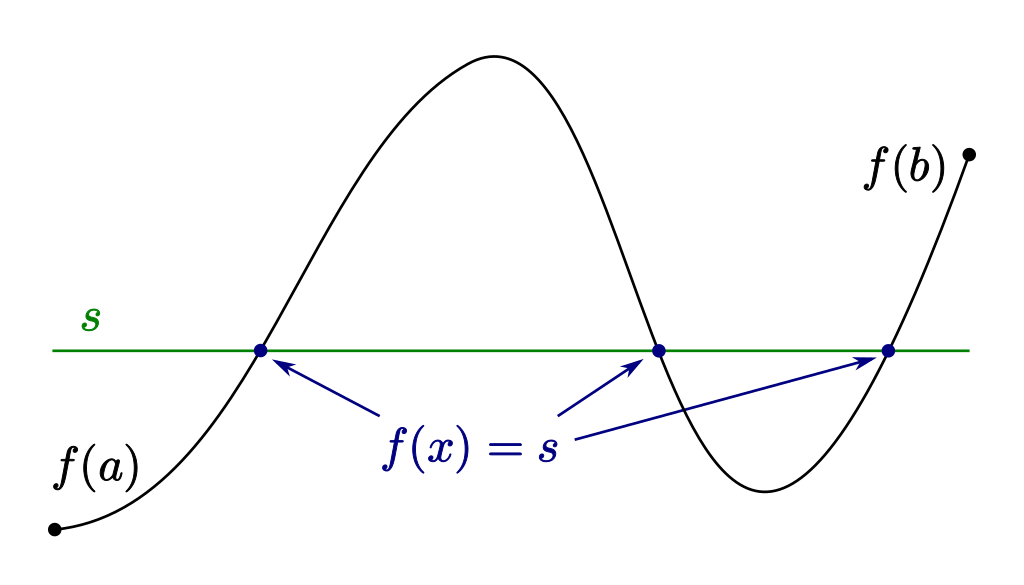
Real-World Motivation
To illustrate, consider an elevator moving continuously between floors. It starts at the first floor and ends at the sixth floor. Because there is no teleportation, the elevator passes through the second, third, fourth, and fifth floors. In mathematical terms, it achieved all intermediate floor values.
Example 1: Finding a Root (Step-by-Step)
Problem Setup
Consider the polynomial function f(x) = x^3 - 3x + 1 over the interval [0, 2]. Evaluate the function at the endpoints:
- f(0) = 0^3 - 3(0) + 1 = 1
- f(2) = 2^3 - 3(2) + 1 = 8 - 6 + 1 = 3
Note that both f(0) and f(2) are positive. This example is slightly different from the typical “opposite signs” scenario, but it can still illustrate a value between 1 and 3.
Apply the IVT
- Confirm Continuity: f(x) = x^3 - 3x + 1 is a polynomial, so it is continuous everywhere, including [0, 2].
- Identify f(a) and f(b): Here, f(0) = 1 and f(2) = 3.
- Choose d between f(0) and f(2): Suppose there is a desire to find a point where the function equals 2 (which lies between 1 and 3).
- Conclude Existence: By the Intermediate Value Theorem, there must be some c in [0, 2] such that f(c) = 2.
Therefore, there is a number c in [0, 2] that solves x^3 - 3x + 1 = 2.
Practice Problem (Example of Intermediate Value Theorem):
Determine if there is a point c in [0, 2] such that f(c) = 1.5 for the function f(x) = x^3 - 3x + 1.
Solution:
- Check continuity: The function is continuous.
- Check f(0) and f(2): They are 1 and 3 respectively.
- Since 1.5 is between 1 and 3, the IVT guarantees a point c where f(c) = 1.5.
Example 2: Intermediate Range Value (Step-by-Step)
Problem Setup
Consider f(x) = \sin x on the interval [-\frac{\pi}{2}, \frac{\pi}{2}]. Observe that:
- f\bigl(-\frac{\pi}{2}\bigr) = -1
- f\bigl(\frac{\pi}{2}\bigr) = 1
Suppose there is an interest in finding a point c where f(c) = 0.5.
Apply the IVT
- Confirm Continuity: The function \sin x is continuous for all real numbers. Over \bigl[-\frac{\pi}{2}, \frac{\pi}{2}\bigr], there are no gaps.
- Evaluate Endpoints:
- f\bigl(-\frac{\pi}{2}\bigr) = -1
- f\bigl(\frac{\pi}{2}\bigr) = 1
- Verify d Is Between f(a) and f(b): The value 0.5 lies between -1 and 1.
- Guarantee Existence of c: By the IVT, there must be a c in \bigl[-\frac{\pi}{2}, \frac{\pi}{2}\bigr] such that \sin c = 0.5.
Intermediate Value Theorem Practice Problems
On the interval [0, \pi], the function g(x) = \sin x ranges from g(0) = 0 to g(\pi) = 0. Is there a point c in [0, \pi] for which g(c) = 0.8?
Solution:
- Check continuity: \sin x is continuous.
- Evaluate endpoints: Both are 0 at x = 0 and x = \pi.
- Check for intermediate values: Because the maximum of \sin x on [0, \pi] is 1 (at \frac{\pi}{2}), the range includes 0.8.
- Conclusion: By the Intermediate Value Theorem, there must be a number c in [0, \pi] where \sin c = 0.8.
Common Pitfalls and Tips
- Misunderstanding continuity can lead to incorrect assumptions.
- Ensure that the desired value truly lies between f(a) and f(b).
- Always use the correct order for a and b. If f(a) is larger than f(b), adjust the viewpoint accordingly.
Quick Reference Chart (Vocabulary and Definitions)
| Term | Definition |
| Continuous Function | A function with no breaks, jumps, or holes in its domain on [a, b] |
| Intermediate Value Theorem (IVT) | If f is continuous on [a, b], then it takes all intermediate values |
| Closed Interval [a, b] | All real numbers x such that a ≤ x ≤ b |
| f(a) and f(b) | The function values at the endpoints a and b |
| c in [a, b] | Some point between a and b |
| d Between f(a) and f(b) | A value lying between the output at a and the output at b |
Conclusion
The Intermediate Value Theorem is central in both pre-calculus and AP® Calculus AB-BC settings. It answers important questions such as “What is the intermediate value theorem and how does continuity affect it?” By ensuring that a function is continuous on a closed interval, the IVT guarantees that any value lying between f(a) and f(b) will occur at some point. This principle is essential for solving equations, verifying the presence of roots, and exploring a function’s range.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
- 1.15 Connecting Limits at Infinity and Horizontal Asymptotes
- 2.1 Defining Average and Instantaneous Rates of Change at a Point
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








