The work-energy theorem is a cornerstone of physics, connecting the concepts of work and energy in a meaningful way. Understanding this theorem is crucial for students preparing for the AP® Physics 1 exam. It helps in analyzing and solving problems involving energy changes due to forces.
What We Review
What Is Work in Physics?
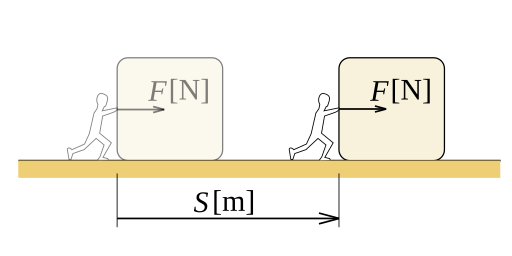
Work in physics is not just about doing chores; it’s about how force causes movement. The concept is defined as the transfer of energy through motion. The mathematical formula to calculate work is:
W = F d \cos(\theta)Here:
- W is the work done (measured in joules, J)
- F is the force applied (in newtons, N)
- d is the distance over which the force is applied (in meters, m)
- \theta is the angle between the force and the direction of movement
Example 1: Calculating Work Done by a Force
Imagine pushing a box with a force of 20 N, moving it 5 meters across the floor at an angle of 0°.
- Given: F = 20 \text{ N}, d = 5 \text{ m}, \theta = 0^\circ
- Calculation: W = 20 \cdot 5 \cdot \cos(0^\circ) = 100 \text{ J}
Therefore, the work done is 100 joules.
Understanding Energy
Energetics is at the heart of physics. Energy is defined as the capacity to do work. It can take many forms, but in the realm of the work-energy theorem, kinetic and potential energy are most pertinent:
- Kinetic Energy (K): Energy of motion, given by K = \frac{1}{2} m v^2
- Potential Energy (U): Energy stored due to position, like gravitational potential energy
The Work-Energy Theorem Explained
The work-energy theorem elegantly relates work done on an object to its kinetic energy change. The theorem’s formula is:
\Delta K = \sum_i W_iThis states that the change in kinetic energy (\Delta K) of an object equals the total work done by all forces.
Example 2: Applying the Work-Energy Theorem
Consider a car accelerating along a straight path. If the engine does 5000 J of work to accelerate the car, and friction does 2000 J of work against it, find the change in kinetic energy.
- Total work done: \Delta K = 5000 \text{ J} - 2000 \text{ J} = 3000 \text{ J}
Thus, the car’s kinetic energy increases by 3000 joules.
Conservative vs. Nonconservative Forces
Forces are either conservative or nonconservative.
- Conservative Forces: These include gravity and spring forces. Their work does not depend on the path and can be fully recovered.
- Nonconservative Forces: Examples are friction and air resistance. Their work depends on the path and often dissipates as heat.
Example 3: Comparing Work Done by Forces
A skier moves down a hill. Gravity does 2000 J of work, while friction does -500 J.
- Gravity (conservative): Path-independent, work done is recoverable.
- Friction (nonconservative): Path-dependent, work is lost to heat.
The Role of Friction
Friction converts mechanical energy into thermal energy, affecting total energy calculations. For friction, the formula is:
\Delta E_{\text{mech}} = F_f d \cos(\theta)Example 4: Calculating Work Done Against Friction
A box slides across the floor with a friction force of 10 N over 8 meters.
- Given: F_f = 10 \text{ N}
- Work done by friction: W = 10 \cdot 8 = 80 \text{ J}
This means it loses 80 joules as heat.
Work Done by a Variable Force
When the force is not constant, calculate work using the area under a force vs. displacement graph.
Practical Applications of the Work-Energy Theorem
The work-energy theorem applies to many real-life scenarios, from engineering to everyday movements like pushing a shopping cart. Understanding this theorem aids in designing efficient machines and solving various physics problems.
Summary of Key Concepts: Work-Energy Theorem
- Work: Transfer of energy through force; W = F d \cos(\theta)
- Kinetic Energy: Energy of motion; work done causes change.
- Conservative versus Non-Conservative Forces: Different characteristics and effects on energy.
- Friction: Alters mechanical energy, usually reducing kinetic energy.
Mastering the work-energy theorem is essential for success in AP® Physics 1. It offers insights into the interaction between forces and energy, forming a foundation for analyzing physical systems.
| Term | Definition |
| Work | Transfer of energy by force over distance |
| Kinetic Energy (K) | Energy of motion; K = \frac{1}{2} m v^2 |
| Potential Energy (U) | Stored energy due to position |
| Conservative Force | Force where work done is path-independent |
| Nonconservative Force | Force where work done is path-dependent |
| Friction | Force opposing motion, transforming energy to heat |
Sharpen Your Skills for AP® Physics 1
Are you preparing for the AP® Physics 1 test? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world physics problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Physics 1 exam?
Albert has hundreds of AP® Physics 1 practice questions, free response, and full-length practice tests to try out.








