Series are infinite sums of terms that help reveal patterns, behaviors, and solutions in advanced mathematics. In particular, determining whether a series converges or diverges is a key step in understanding its overall behavior. An alternating series is a series that switches between positive and negative terms, which adds an interesting twist to the question of convergence. The alternating series test is often introduced in AP® Calculus AB-BC courses because it provides a straightforward way to determine if certain types of alternating series converge.
This post explains the basics of an alternating series, why convergence is important, and how to use the alternating series test. It includes simple explanations and examples designed for high school students preparing for AP® Calculus AB-BC.
What We Review
Understanding Alternating Series
What Makes a Series “Alternating”?
An alternating series is a series where consecutive terms alternate in sign. So one term is positive, the next is negative, and then it repeats. This pattern can be expressed as: \sum_{n=1}^\infty (-1)^n a_n or \sum_{n=1}^\infty (-1)^{n+1} a_n depending on whether the first term is positive or negative.
Imagine a line of people facing opposite directions: the first person faces right (positive), the next faces left (negative), then the next right, then left, and so on. This back-and-forth stance captures the idea of “alternation” in this type of series.
Importance of Convergence in Alternating Series
A series converges when its partial sums approach a finite number. For alternating series, this usually depends on two main conditions. First, each new term should have a smaller magnitude than the previous term. Second, each term should get closer and closer to zero as n increases. Without these conditions, the sum may not settle on a definite value. Therefore, a specialized test is needed to capture these behaviors in alternating series, especially in the context of alternating series calc bc.
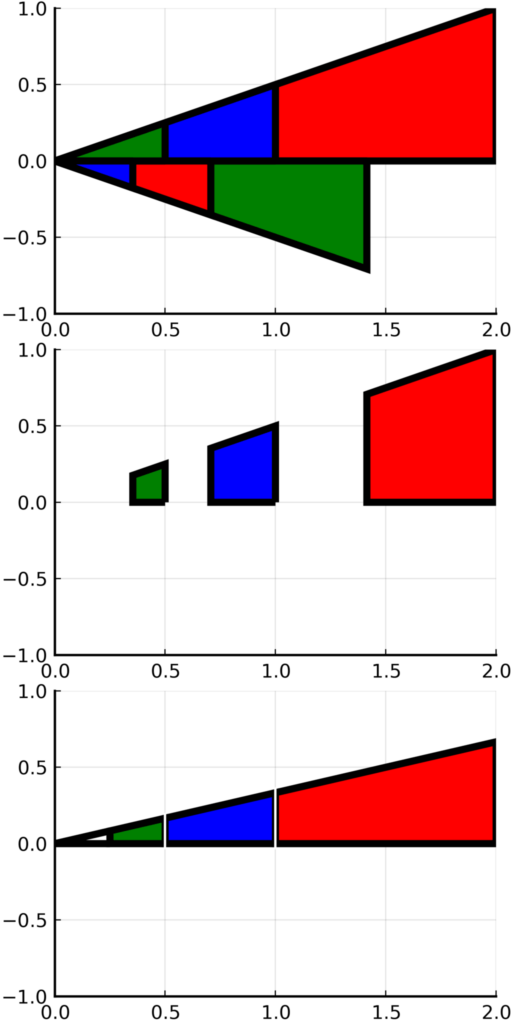
The Alternating Series Test for Convergence
Statement of the Test
The alternating series test says that if a series has terms (-1)^{n} b_n(or a similar pattern of alternating signs), it will converge if:
- The absolute values of the terms b_n get smaller as n increases. In other words, b_{n+1} \leq b_n for all n (meaning the sequence {b_n} is eventually decreasing).
- The limit of b_n is zero. That is, \lim_{n \to \infty} b_n = 0.
For an AP® Calculus AB-BC student, these two conditions are the key requirements in identifying series that converge by the alternating series test.
Step-by-Step Application
- Identify the pattern of positive and negative terms.
- Check if the magnitude of each term is smaller than the one before it.
- Calculate the limit of b_n. If it goes to zero, then the second condition is satisfied.
- If both conditions hold, conclude the series converges.
Example 1: Applying the Alternating Series Test
Consider the series: \sum_{n=1}^\infty \frac{(-1)^n}{n}.
Step-by-Step Solution:
- First, notice that the terms alternate in sign because of (-1)^n. Hence, it is an alternating series.
- The absolute value of the nth term is \frac{1}{n}. As n increases, \frac{1}{n} gets smaller. Therefore, the terms decrease in absolute value.
- Next, find the limit of \frac{1}{n} as n \to \infty: \lim_{n \to \infty} \frac{1}{n} = 0.
- Since all conditions are met, the alternating series test indicates that this series converges.
Why the Alternating Series Test Works
The alternating series test is based on the idea that each positive term is counterbalanced by a negative term, while the magnitude of these terms steadily decreases. Therefore, if the sequence of absolute values shrinks to zero, the partial sums “zigzag” closer and closer to a specific number. This logic shows that no large jumps can derail the sum, ensuring the overall series converges.
Additional Example: Variety in Application
Example 2: A Different Alternating Series
Consider the series: \sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n^2}.
Step-by-Step Solution:
- Again, there is an alternating factor (-1)^{n+1}, which makes the terms positive, then negative, then positive, and so on.
- The absolute value of each term is \frac{1}{n^2}. Since \frac{1}{n^2} decreases as n increases, that condition is satisfied.
- Find the limit as n \to \infty: \lim_{n \to \infty} \frac{1}{n^2} = 0.
- Therefore, because both conditions (terms decreasing in absolute value and limit going to zero) are met, the series converges by the alternating series test.
Common Mistakes and What to Watch Out For
- Forgetting to check if the absolute values of terms decrease. Sometimes, terms might alternate in sign but not shrink in size.
- Overlooking the limit condition. Even if the terms alternate, if they do not approach zero, the series will not converge.
Comparison with Other Convergence Tests
Sometimes, other convergence tests like the Ratio Test or the Integral Test may be more appropriate. However, the alternating series test is usually the simplest route for alternating series where terms fit its basic conditions. It is especially useful for alternating series calc bc topics that appear on AP® exams, where efficiency often matters.
The Ratio Test involves taking the ratio of successive terms to see if it is less than 1, while the Integral Test converts the series into an integral to check for convergence. By contrast, the alternating series test focuses specifically on the sign pattern and decreasing term magnitudes.
Quick Reference Chart
Below is a concise list of important definitions and features:
| Term | Definition/Example |
| Alternating Series | Definition: A series whose terms switch between positive and negative. Example: \sum_{n=1}^\infty (-1)^n a_n. |
| Limit | Definition: The value that a function (or sequence) approaches as its input (or index) goes to infinity. Example: \lim_{n \to \infty} \frac{1}{n} = 0. |
| Convergence | Definition: When a series or sequence approaches a finite value. Key Point: The alternating series test requires shrinking terms and a zero limit. |
Conclusion
An alternating series is distinguished by its ever-changing sign. By checking two clear conditions—terms shrinking in absolute value and approaching zero—students can apply the alternating series test to decide if these back-and-forth sums converge. This framework is important for AP® Calculus AB-BC, where knowing when to use a specific convergence test can simplify the process of understanding infinite series.
When analyzing higher-level series, a methodical approach reduces mistakes and confusion. Therefore, focusing on each step—verifying the sign pattern, making sure terms decrease, and confirming the limit—sets a strong foundation for consistent results. With this knowledge, students can feel more confident tackling alternating series problems on exams and in real-world applications.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.








