Power series are central to many concepts in calculus. They help express complicated functions as sums of simpler terms. This is useful because, near a specific point, a power series can approximate a function remarkably well. In advanced classes like AP® Calculus AB-BC, the representation of power series often appears in problems involving differentiation and integration.

This article explores what a power series is, outlines methods to find a power series representation for the function, and demonstrates these methods step by step. It also offers practical examples and ends with a quick reference chart of important terms. Mastering these essentials builds a strong foundation for deeper calculus studies.

What Is a Power Series?

Power series are infinite sums of powers of a variable, typically $x$, about a certain point (often $0$). The most common form looks like: $\displaystyle \sum_{n=0}^{\infty} a_n (x-c)^n$

Here, $c$ is the center of the expansion, and the coefficients $a_n$ can be constants determined by the function’s behavior.

When asked, “What is the power series for a specific function?” or “How can a function be represented using a series?”, the goal is to rewrite the function as a sum of terms in increasing powers of $x-c$. This representation of power series makes it easier to analyze the function’s behavior near $c$ and perform advanced operations, such as differentiation and integration.

Methods to Find a Power Series Representation for the Function

There are multiple approaches to find a power series representation for the function:

Using Known Series (Geometric and Others)

• The geometric series is one of the most popular starting points: $\displaystyle \frac{1}{1-r} = \sum_{n=0}^{\infty} r^n$
• By substituting a specific expression in place of $r$, it becomes possible to rewrite many functions in series form.
• After substitution, simplify the expression to ensure the series lines up with the function’s terms.

Power Series by Differentiation

• Power series by differentiation involves starting with a known series, such as the geometric series.
• Differentiate term by term to obtain a new series that corresponds to the derivative of the original function.
• This technique is especially helpful in AP® Calculus AB-BC problems because it simplifies the process of finding higher-order derivatives in series form.

Integrating Power Series

• Integrating power series follows a similar idea: take a known series and integrate each term.
• Always recall that an integration constant may be required.
• Integrating power series is useful in obtaining antiderivatives or checking definite integrals under certain convergence conditions.

Substitution and Algebraic Processes

• Some functions do not immediately match a standard series. Substitution or algebraic manipulation is often needed.
• Take care when replacing variables or constants to ensure correct alignment with the center of the series.

Example 1: Constructing a Series Through a Geometric Expansion

Consider the function:

The goal is to find a power series representation for the function around $x = 0$. Notice that it matches the form of a geometric series $\frac{1}{1-r}$ if $r=2x$. Follow these steps:

1. Recognize that $\frac{1}{1 - 2x}$ resembles $\frac{1}{1-r}$ with $r=2x$.
2. Substitute $r=2x$ into the geometric series: $\displaystyle \frac{1}{1 - 2x} = \sum_{n=0}^{\infty} (2x)^n$
3. Simplify the expression: $\displaystyle \sum_{n=0}^{\infty} (2x)^n = \sum_{n=0}^{\infty} 2^n x^n$

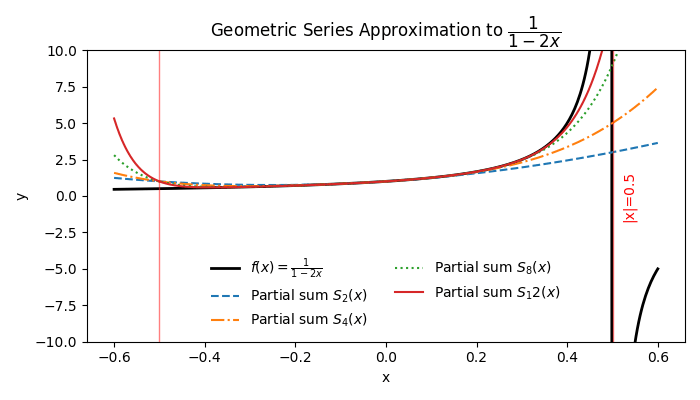
Hence, the power series is: $\displaystyle \sum_{n=0}^{\infty} 2^n x^n$

Example 2: Power Series by Differentiation

Start with the known series for $\frac{1}{1 - x}$, which is: $\displaystyle \frac{1}{1 - x} = \sum_{n=0}^{\infty} x^n$

Differentiate both sides to find the power series by differentiation:

1. Differentiate the left-hand side: $\displaystyle \frac{d}{dx}\left(\frac{1}{1-x}\right) = \frac{1}{(1-x)^2}$
2. Differentiate the right-hand side term by term: $\displaystyle \frac{d}{dx}\left(\sum_{n=0}^{\infty} x^n\right) = \sum_{n=0}^{\infty} \frac{d}{dx}(x^n)$ $\displaystyle = \sum_{n=1}^{\infty} n x^{n-1}$(Note that the $n=0$ term is a constant and disappears upon differentiation.)
3. Thus, the new representation of the derivative is: $\displaystyle \frac{1}{(1-x)^2} = \sum_{n=1}^{\infty} n x^{n-1}$

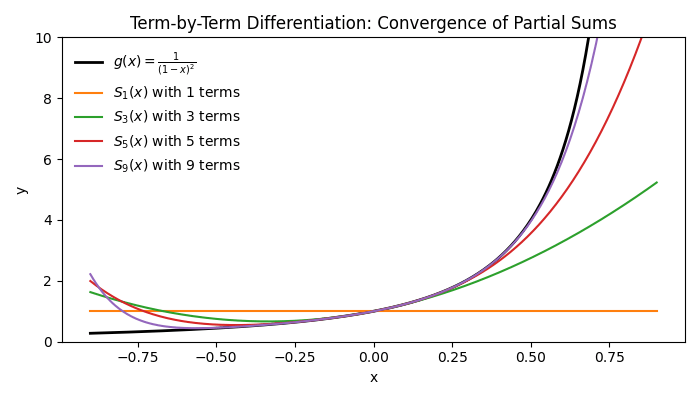
Example 3: Integrating a Known Power Series

Consider the same starting series: $\displaystyle \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n$

Now, interpret integrating power series by integrating both sides:

1. Integrate the left-hand side with respect to $x$: $\displaystyle \int \frac{1}{1-x} , dx = -\ln(1-x) + C$
2. Integrate the right-hand side term by term: $\displaystyle \int \sum_{n=0}^{\infty} x^n , dx = \sum_{n=0}^{\infty} \int x^n , dx = \sum_{n=0}^{\infty} \frac{x^{n+1}}{n+1} + C$
3. Therefore, the final integrated form can be written as: $\displaystyle -\ln(1-x) + C = \sum_{n=0}^{\infty} \frac{x^{n+1}}{n+1} + C$

Adjust $C$ if a definite integral or initial condition is given.

Quick Reference Chart: Key Terms and Definitions

Conclusion

A power series is a helpful way to analyze functions in a form that highlights each power of $x$. The representation of power series allows students to see local behavior more clearly and perform operations such as power series by differentiation and integrating power series. In addition, it is often possible to use a power series calculator to check expansions or test partial results.

This article covered the basics of what is the power series, how to find a power series representation for the function using geometric expansions, and how to transform a known series through differentiation or integration. Each technique builds upon the previous one, creating a versatile set of tools for further exploration in calculus. Practicing these methods fosters greater comfort with advanced calculus topics and prepares learners for more complicated analysis.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

• 10.13 Radius and Interval of Convergence of Power Series
• 10.14 Finding Taylor or Maclaurin Series for a Function

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.