Introduction

Derivatives are a major concept in calculus because they capture how functions change. They answer questions about rates of change in everyday situations, like how quickly a car speeds up or how fast a population grows. These ideas, including derivatives of trig functions, matter in physics, biology, economics, and many other fields.

This article focuses on derivatives of trig functions and logs, which feature prominently in AP® Calculus AB-BC. According to the framework (FUN-3.A.4 and LIM-3.A.1), understanding these derivatives is essential for deeper analysis of functions. The goal here is to show clear, step-by-step approaches that make the derivative of trig functions and the derivative of log feel more straightforward.

Fundamental Derivative Rules for Trig Functions

Knowing the derivatives of trig functions is key for solving many exam questions. Start by memorizing the basic derivatives of sine and cosine, then extend to other trig functions.

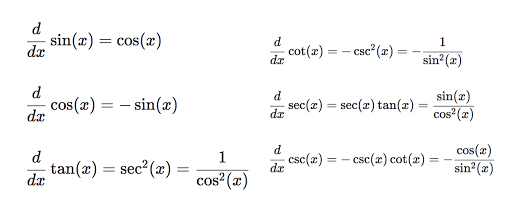
Derivative of Sin x

When asked about the derivative of sin x, recall that: \frac{d}{dx}[\sin x] = \cos x

This comes from investigating how sin x behaves in infinitesimally small intervals. A standard limit-based approach proves this formally. However, the known formula is used most often.

Step-by-Step (Limit Outline)

1. Write the limit definition of the derivative: \lim_{h \to 0} \frac{\sin(x+h) - \sin(x)}{h}
2. Use the sine addition formula: \sin(x+h) = \sin x \cos h + \cos x \sin h
3. Simplify and separate like terms.
4. As h \to 0, \sin h \approx h and \cos h \approx 1.
5. The expression simplifies, confirming the result is \cos x.

Derivative of Cos x

Similarly, the derivative of cosine is: \frac{d}{dx}[\cos x] = -\sin x

A limit-based method also supports this negative sign. In practice, it can be remembered that cosine shifts the sine wave by 90 degrees, leading to the negative sign.

Step-by-Step (Limit Outline)

1. Use the limit definition: \lim_{h \to 0} \frac{\cos(x+h) - \cos x}{h}
2. Apply the cosine addition formula: \cos(x+h) = \cos x \cos h - \sin x \sin h
3. Simplify, observing that \cos h \approx 1 and \sin h \approx h as h \to 0.
4. A factor of -\sin x appears, giving the final derivative.

Other Trig Derivatives

It also helps to memorize the other standard derivatives of trig functions:

• \frac{d}{dx}[\tan x] = \sec^2 x
• \frac{d}{dx}[\csc x] = -\csc x \cot x
• \frac{d}{dx}[\sec x] = \sec x \tan x
• \frac{d}{dx}[\cot x] = -\csc^2 x

Memorizing each derivative of trig functions makes it easier to work through integrals and more advanced calculus problems. Practicing them regularly can help build speed and confidence.

Logarithmic and Exponential Derivatives

Logs and exponentials are ubiquitous in science and math. Their derivatives have simple patterns that make them easier to manipulate in calculus problems.

Derivative of log x (e.g., ln x)

The derivative of log to the base e (ln x) is: \frac{d}{dx}[\ln x] = \frac{1}{x}

This appears frequently in optimization problems and growth models. The limit definition often involves a known limit \lim_{u \to 0} \frac{\ln(1+u)}{u} = 1, so the result emerges cleanly.

Step-by-Step (Limit Outline)

1. Start with: \lim_{h \to 0} \frac{\ln(x+h) - \ln x}{h}
2. Rewrite as: \lim_{h \to 0} \ln\left(\frac{x+h}{x}\right) \cdot \frac{1}{h}
3. Notice that \frac{x+h}{x} = 1 + \frac{h}{x}.
4. Apply limit properties, and recognize a standard limit form, concluding the limit simplifies to \frac{1}{x}.

Derivative of Exponential Functions

The derivative of e^x remains e^x. More specifically: \frac{d}{dx}[e^x] = e^x

For other bases, such as a^x, the chain rule introduces a constant factor \ln a. In other words, \frac{d}{dx}[a^x] = a^x \ln a

This rule shows how any exponential’s rate of change depends on its natural logarithm.

Using Limit Definitions Strategically (LIM-3.A.1)

Sometimes, a limit problem looks complicated, yet it matches the definition of the derivative. Recognizing a form like \frac{f(x+h) - f(x)}{h}as h \to 0 can save time.

Example: Evaluating a Trig Limit

Consider the limit: \lim_{h \to 0} \frac{\sin(\pi/2 + h) - \sin(\pi/2)}{h}

Step-by-Step Approach

1. Identify that this limit fits \frac{f(\pi/2 + h) - f(\pi/2)}{h} with f(x) = \sin x.
2. The known derivative of \sin x is \cos x.
3. Therefore, evaluate \cos(\pi/2) = 0.
4. The limit is 0, so a tricky-looking problem simplifies quickly.

Worked Examples

Example 1: Derivative of sin x

Find the derivative of \sin x.

1. Use the standard rule directly: \frac{d}{dx}[\sin x] = \cos x.
2. (Optional) Confirm by limit definition if needed.
3. Final answer: \cos x.

Example 2: Derivative of cos x

Find the derivative of \cos x.

1. Apply the standard formula: \frac{d}{dx}[\cos x] = -\sin x.
2. Verify with the limit definition for a deeper understanding.
3. Final answer: -\sin x.

Example 3: Derivative of ln x

Find the derivative of \ln x.

1. Recall the known formula: \frac{d}{dx}[\ln x] = \frac{1}{x}.
2. Or, use limit methods involving \ln(1 + u) expansions.
3. Final answer: \frac{1}{x}.

Quick Reference Chart

This chart offers a quick look at the derivative of trig functions, as well as the derivative of log and exponential functions.

Function	Derivative	Key Point
\sin x	\cos x	Peak changes at \pi/2, 3\pi/2
\cos x	-\sin x	Shifted sine wave
\tan x	\sec^2 x	Infinite slope at \pi/2, 3\pi/2
\ln x	\frac{1}{x}	Logs grow slowly
e^x	e^x	Self-derivative

Conclusion

In summary, derivatives of trig functions and logarithms are central to mastering AP® Calculus AB-BC. The derivative of sin x is cos x, while the derivative of cosine is –sin x. Likewise, the derivative of ln x is 1/x. These fundamental facts appear in many exam questions and real-life rate-of-change problems.

Consistent practice builds a strong foundation. Memorizing key derivatives and using the limit definition when necessary will develop both speed and clarity. By thoroughly understanding these concepts, calculus students can learn to see how functions change and take on advanced applications with confidence.

Sharpen Your Skills for AP® Calculus AB-BC

Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

Need help preparing for your AP® Calculus AB-BC exam?

Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.