What We Review
Introduction: What Is the Chain Rule?
Many students wonder, “What is the chain rule?” It is a powerful tool in calculus that helps find the derivative of a composite function. In AP® Calculus AB-BC, this concept is crucial because so many real-world problems involve functions nested within each other.
This post will explain the basics of composite functions, walk through the chain rule step by step, and show how it applies to real examples like the derivative of sec²(2x). By the end, it should be clear why the chain rule is at the heart of derivative of composite function problems in calculus.
Understanding Composite Functions
A composite function appears when one function sits inside another. For instance, if one function describes the temperature over time, and another function converts temperature to profit, the overall profit depends on time through both functions.
In simpler mathematical terms, a composite function can be written as f(g(x)). It means “apply g(x) first, then apply f to the result of g(x).” This nesting occurs regularly in science and economics. Therefore, recognizing and handling these composites is key.
Example 1: A Simple Composite Function
Let f(x) = x^2 + 1 and g(x) = x + 3. Form the composite h(x) = f(g(x)).
Step-by-step Solution:
- Write down the composite: h(x) = f(g(x)) = f(x + 3).
- Substitute g(x) into f: h(x) = (x + 3)^2 + 1.
- Simplify if needed: h(x) = x^2 + 6x + 9 + 1 = x^2 + 6x + 10.
Introduction to the Chain Rule: What Is the Chain Rule?
When working with a derivative of composite function, the chain rule is essential. The chain rule states:
\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x).In simpler terms, differentiate the outer function first, then multiply by the derivative of the inner function. This formula is the foundation for handling complicated functions like (x^3 + 2)^4 or even trigonometric functions with multiple layers. The graphic below shows a funny interpretation of applying the chain rule to a composite function with 4 inner layers.
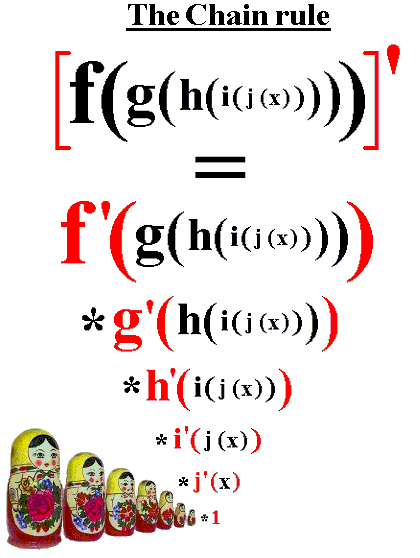
Example 2: Demonstrating the Chain Rule
Consider the function y = (x^3 + 2)^4. The “outer” function is something raised to the fourth power, and the “inner” function is x^3 + 2.
Step-by-step Solution:
- Label the inner function as u(x) = x^3 + 2.
- The outer function can be seen as f(u) = u^4.
- Find the derivative of f(u) = u^4 with respect to u: f'(u) = 4u^3.
- Find the derivative of the inner function u(x) = x^3 + 2 with respect to x: u'(x) = 3x^2.
- Apply the chain rule: \frac{dy}{dx} = f'(u(x)) \cdot u'(x) = 4(x^3 + 2)^3 \cdot 3x^2.
- Simplify: \frac{dy}{dx} = 12x^2 (x^3 + 2)^3.
Detailed Example: Derivative of sec²(2x)
Trigonometric functions often involve layers, making them perfect for chain rule practice. The derivative of composite function \sec^2(2x) is a common AP® Calculus AB-BC question. Recognizing the inner function as 2x and the outer function as \sec^2(u) helps keep things clear.
Example 3: Finding \frac{d}{dx}[\sec^2(2x)]
- Identify the inner function: u(x) = 2x.
- Recognize the outer function: f(u) = \sec^2(u).
Step-by-step Solution:
- Recall that \frac{d}{du}[\sec^2(u)] = 2\sec(u)\cdot\sec(u)\tan(u). However, many use a slightly shorter approach: \frac{d}{du}[\sec(u)] = \sec(u)\tan(u), so by extension,\frac{d}{du}[\sec^2(u)] = 2\sec(u)\cdot \frac{d}{du}[\sec(u)] = 2\sec(u)\bigl(\sec(u)\tan(u)\bigr) = 2\sec^2(u)\tan(u).
- Multiply by the derivative of the inner function u'(x) = 2.
- Hence,\frac{d}{dx}[\sec^2(2x)] = 2\sec^2(2x)\tan(2x) \cdot 2.
- Combine everything: \frac{d}{dx}[\sec^2(2x)] = 4\sec^2(2x)\tan(2x).
This process neatly illustrates that even when working with trigonometric functions, the chain rule can handle nested expressions.
Putting It All Together
The derivative of composite function problems show up in many forms. Sometimes, there may be more than two layers, such as \sin\bigl(e^{2x^3}\bigr). However, the logic remains consistent: differentiate the outer function, then multiply by the derivative of everything inside it.
Remember these tips:
- Identify the outer function first.
- Label the inside as u(x).
- Differentiate f(u) with respect to u.
- Multiply by \frac{du}{dx}.
It may take practice, but this rule soon becomes second nature.
Quick Reference Chart: Key Vocabulary and Definitions
| Term | Definition |
| Chain Rule | A formula to find the derivative of a composite function: \frac{d}{dx}[f(g(x))] = f'(g(x))g'(x) |
| Composite Function | A function formed by substituting one function into another, often written as f(g(x)) |
| Outer Function | The function that operates on the result of an inner function |
| Inner Function | The function inserted inside another function |
| Derivative | The rate of change of a function with respect to its variable |
Conclusion
The chain rule gives the power to tackle the derivative of composite function problems, whether they look like a straightforward polynomial inside a power or a trigonometric function like \sec^2(2x). By breaking a function into inner and outer parts and applying the chain rule, most derivatives become more approachable.
Keeping these fundamentals in mind will help with success in AP® Calculus AB-BC and beyond. With enough practice, identifying the right layers and applying the chain rule will feel natural, no matter how complex the function appears.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.
