Calculus revolves around the derivative, a tool that measures the rate of change of a function. This concept is central to AP® Calculus AB-BC because it forms the foundation of many advanced topics. However, it is also important to understand the question, “When does a derivative not exist?” According to the AP® Calculus Curriculum, specifically FUN-2.A.1 and FUN-2.A.2, continuity and differentiability are closely connected. Therefore, students who grasp these connections can quickly identify situations where derivatives fail to exist.
What We Review
The Link Between Continuity and Differentiability
Review of Continuity
Continuity is a simple but powerful idea. A function f(x) is continuous at a point x = a if the limit from both sides—left and right—matches the value f(a). In other words, the function has no sudden jumps or breaks at x = a.
Moreover, if a function is differentiable at a point, then it is automatically continuous at that point. However, continuity alone does not guarantee that the derivative exists, which leads to the next key insight.
Domain Considerations
Sometimes a function is not defined at a certain point. When that happens, the derivative is also not defined there. For example, if f(x) has a domain that excludes x = 2, the derivative cannot exist at x = 2. Therefore, always check whether the function itself is defined before investigating the derivative.
Common Reasons a Derivative Might Not Exist
Sharp Corners and Cusps
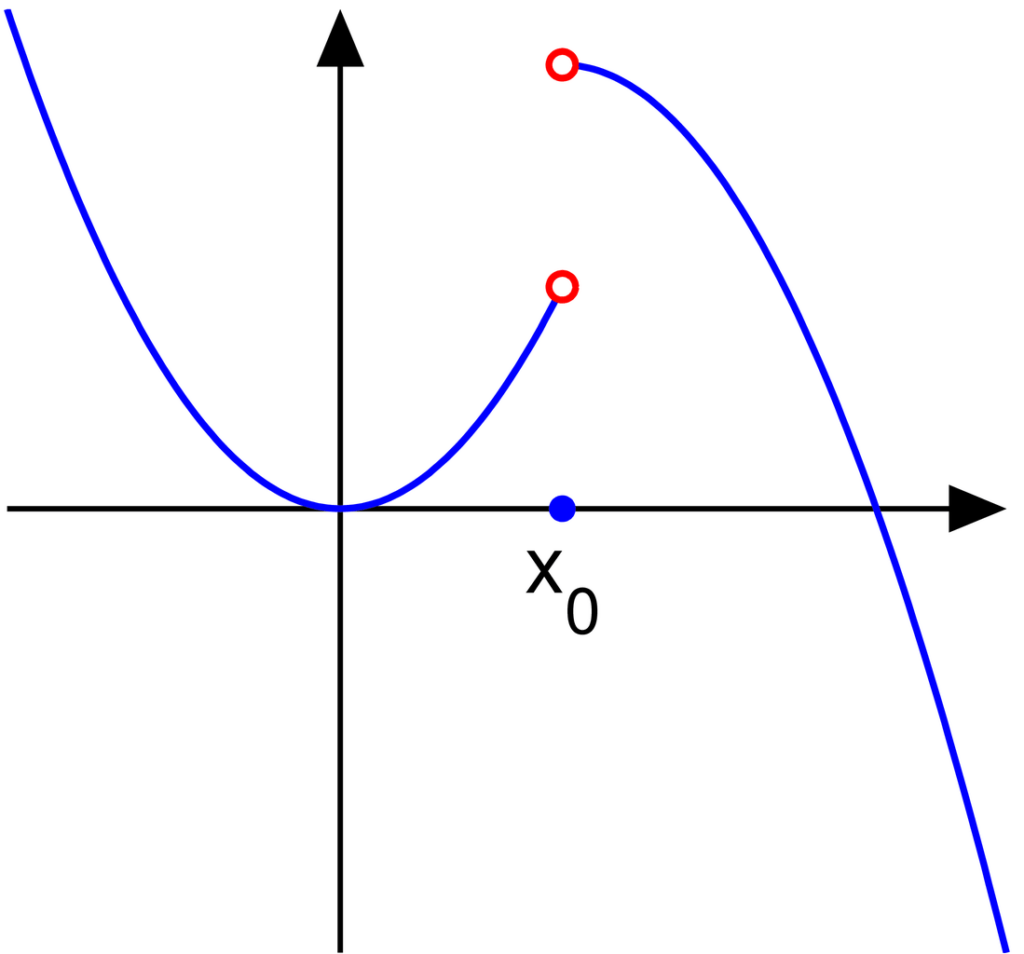
When does a derivative not exist? Two prime examples are at a corner or a cusp. It happens because the slope (or rate of change) from the left side is different from the slope from the right side. A corner creates an abrupt change in direction, so the limits of the derivative from the left and right fail to match.
Vertical Tangent Lines
A vertical tangent line means the slope tends to positive or negative infinity. In such a case, the rate of change grows without bound. This situation implies that the derivative is not defined because a finite slope does not exist at that point.
Discontinuities
When a function is not continuous, its derivative automatically does not exist there. If there is a jump, hole, or any break, the limit from both sides of the function fails to match its value. As a result, the derivative cannot be calculated.
Other Special Situations
Piecewise functions can create issues if the “joining” slopes on each side do not align at the boundary. If the limit of the derivative from the left does not equal the limit of the derivative from the right, the derivative does not exist at that boundary point.
Step-by-Step Examples
Example 1: Function with a Corner
Consider the piecewise function: f(x) =\begin{cases}x & \text{if } x \ge 0 \\-x & \text{if } x < 0\end{cases}
- Notice that f(x) is actually the absolute value function, |x|.
- For x > 0, the derivative is 1, because f(x) = x.
- For x < 0, the derivative is -1, because f(x) = -x.
- At x = 0, the left-hand slope is -1, and the right-hand slope is 1. These two do not match, so the derivative does not exist at that point.
Example 2: Vertical Tangent
Consider the function g(x) = x^{1/3}. Examine the derivative at x = 0.
- The derivative of g(x) = x^{1/3} can be found using power rules for fractional exponents.
- g'(x) = \frac{1}{3} x^{-2/3}.
- As x gets closer to 0, x^{-2/3} becomes larger and larger in magnitude (it goes to infinity in the positive direction for x > 0 and negative direction for x < 0).
- Therefore, at x = 0, the slope blows up to infinity and the derivative is not defined.
Example 3: Discontinuity
Consider the function: h(x) =\begin{cases}x+1 & \text{if } x < 2 \\ x-3 & \text{if } x \ge 2\end{cases}
Determine continuity and differentiability at x = 2.
- For x < 2, h(x) = x + 1. So h(2^-)=2+1=3.
- For x \ge 2, h(x) = x - 3. So h(2^+)=2-3=-1.
- Since 3 \neq -1, the function has a jump at x=2.
- This jump means the function is not continuous, so the derivative at x=2 does not exist.
Quick Reference Chart
| Term | Definition |
| Derivative | The instantaneous rate of change of a function at a specific point. |
| Continuity | A function is continuous at a point if its limit from both sides equals the function’s value at that point. |
| Differentiability | A function is differentiable at a point if the derivative exists at that point. |
| Corner/Cusp | A point where the slope abruptly changes, causing different left and right derivatives. |
| Vertical Tangent | A point where the slope becomes infinitely large (undefined slope). |
| Discontinuity | A break in the function causing a mismatch in the limit from both sides. |
Conclusion
In summary, “When does a derivative not exist?” The most common reasons include sharp corners, cusps, vertical tangents, and discontinuities. Furthermore, functions must be continuous at a point for a derivative to exist there. If a function is not continuous or experiences abrupt changes, the derivative is not defined at that point. These principles arise repeatedly in AP® Calculus AB-BC and provide valuable insights into how functions behave. They also emphasize why continuity is such an important stepping-stone to differentiability.
Sharpen Your Skills for AP® Calculus AB-BC
Are you preparing for the AP® Calculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!
Need help preparing for your AP® Calculus AB-BC exam?
Albert has hundreds of AP® Calculus AB-BC practice questions, free responses, and an AP® Calculus AB-BC practice test to try out.