Introduction

The tangent function is a crucial part of trigonometry, offering insight into the relationship between angles and the slopes of lines. Understanding the tangent function is essential for exploring how angles and slopes connect, particularly using the unit circle and angles in standard position. Read this guide to help you study for section 3.8 The Tangent Function from the AP® Precalculus CED!

Understanding the Tangent Function

Definition and Basic Concept

The tangent function relates an angle in a right triangle to the ratio of two sides. It is defined as follows:

$\tan\theta = \frac{\text{opposite side}}{\text{adjacent side}}$

This function helps us find how steep a line is or understand how quickly something changes.

The Unit Circle and Terminal Rays

The unit circle is a circle with a radius of 1, centered at the origin on a coordinate plane. It serves as a key tool in trigonometry. An angle in standard position starts with its vertex at the origin, and its initial side along the positive $x$-axis. The other side of the angle is called the terminal ray.

Unit Circle with Tangent

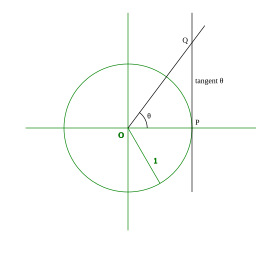
Finding the Point on the Unit Circle

To find the corresponding point $P$ on the unit circle for any angle $\theta$:

1. Place the angle in standard position.
2. Identify where the terminal ray intersects the unit circle.
3. This point $P(x, y)$ is $(\cos\theta, \sin\theta)$.

Example:

For $\theta = 45^\circ$, the terminal ray intersects the unit circle at $P(\sqrt{2}/2, \sqrt{2}/2)$.

Analyzing the Slope of the Terminal Ray

The slope of the terminal ray in the unit circle is the tangent of the angle:

$\tan\theta = \frac{\sin\theta}{\cos\theta}$

Example: Finding the Slope of the Terminal Ray at $135^\circ$

Step 1: Find $\sin 135^\circ$ and $\cos 135^\circ$

The angle $135^\circ$ is in Quadrant II with a reference angle of $45^\circ$:

$\sin 135^\circ = \frac{\sqrt{2}}{2}, \quad \cos 135^\circ = -\frac{\sqrt{2}}{2}$

Step 3: Compute $\tan 135^\circ$

$\tan 135^\circ = \frac{\sin 135^\circ}{\cos 135^\circ} = \frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}} = -1$

Conclusion: The slope of the terminal ray at $135^\circ$ is $-1$, matching the slope of the line $y = -x$.

Relationship Between Tangent, Sine, and Cosine

The Tangent Ratio

The tangent of an angle is the ratio of its sine to its cosine:

$\tan\theta = \frac{\sin\theta}{\cos\theta}$

Understanding Sine and Cosine

In the unit circle, sine and cosine represent the $y$-coordinate and $x$-coordinate of the point where the terminal ray meets the circle.

Example:

Calculate $\tan\theta$ for $\theta = 30^\circ$:

1. $\cos 30^\circ = \sqrt{3}/2$
2. $\sin 30^\circ = 1/2$
3. Therefore, $\tan 30^\circ = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$

Tangent Function Characteristics

Periodicity and Asymptotes

The tangent function is periodic with a period of $180^\circ$ or $\pi$ radians. It is undefined whenever the cosine is zero, which occurs at $\theta = 90^\circ + 180^\circ k$, where $k$ is an integer. These points, called asymptotes, represent angles at which the function shoots off to infinity.

Quick Reference Chart

Conclusion

Understanding the tangent function and its relationship to angles and slopes can deepen comprehension of trigonometry. This knowledge is pivotal not only in math but in various real-world situations. Practice these concepts to master them, and review how the unit circle provides a helpful framework for understanding angles and their trigonometric functions.

Sharpen Your Skills for AP® Precalculus

Are you preparing for the AP® Precalculus exam? We’ve got you covered! Try our review articles designed to help you confidently tackle real-world math problems. You’ll find everything you need to succeed, from quick tips to detailed strategies. Start exploring now!

• 3.6 Sinusoidal Function Transformations
• 3.7 Sinusoidal Function Context and Data Modeling
• 3.8.B The Tangent Function

Need help preparing for your AP® Precalculus exam?

Albert has hundreds of AP® Precalculus practice questions, free responses, and an AP® Precalculus practice test to try out.